Домашние задания по расчету электрических цепей: Методические указания, страница 17

где   ‑ постоянные интегрирования, определяются из начальных условий, отражающих сохранение начальных запасов энергии в емкости  и катушке индуктивности ;

 и  определяются как  корни характеристического уравнения, соответствующего дифференциальному уравнению (6.12)

,                                                                  (6.13)

где 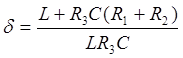‑ коэффициент затухания колебаний в контуре;  ‑ угловая частота незатухающих колебаний.

Решением характеристического уравнения (6.13) являются корни:

.                                                   (6.14)

По их виду можно судить о характере переходного процесса:

‑Если  корни получаются комплексными, сопряженными с отрицательной вещественной частью  где . Тогда переходный процесс носит колебательный характер, и полное решение  уравнения (6.9) принимает вид

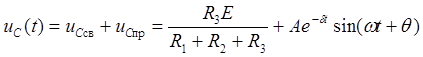.                           (6.15)

Скорость изменения напряжения на конденсаторе

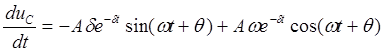.                        (6.16)

Если корни характеристического уравнения отрицательные, вещественные и разные, переходный процесс носит затухающий апериодический характер. Полное решение дифференциального уравнения (6.9) для емкости имеет вид:

.                                            (6.17)

Скорость изменения напряжения на конденсаторе

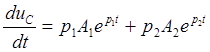.                                              (6.18)

Поскольку (для нашего варианта) корни характеристического уравнения (6.13) являются комплексными (), то свободная составляющая решения имеет характер затухающих во времени колебаний.

I.4. Определение постоянных интегрирования. Постоянные интегрирования  (А₁, А₂) в зависят от параметров цепи, ЭДС и момента включения (). Постоянные могут быть определены посредством решения алгебраических уравнений (6.17) и (6.18) с учетом начальных условий. Поэтому подставим в оба выражения . Числовые значения левой части уравнений определены в начальных условиях (см. выше, п. I.2). В результате, получаем систему алгебраических уравнений:

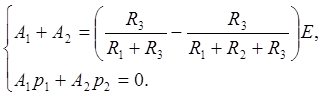                                      (6.19)

Решение системы уравнений позволяет найти постоянные интегрирования А₁ и А₂.

В случае, когда корни характеристического уравнения комплексно сопряженные, воспользуемся уравнениями (6.15) и (6.16). Тогда система уравнений для определения постоянных интегрирования принимает вид

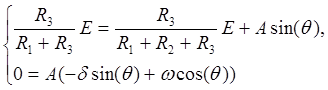                                  (6.20)

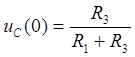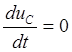где  и  определены в начальных условиях п.I.2. Решая систему уравнений (6.20), определяем .

После подстановки постоянных интегрирования  в формулу (6.15) (или (6.17)), получаем окончательное значение напряжения на емкости. Полученные значения проверяем задавая .

Для варианта 30: , В.

Окончательное значение напряжения на емкости:

.

График напряжения  приведен на рис. 6.4.

Остальные токи и напряжения определяются с помощью системы уравнений (6.1).

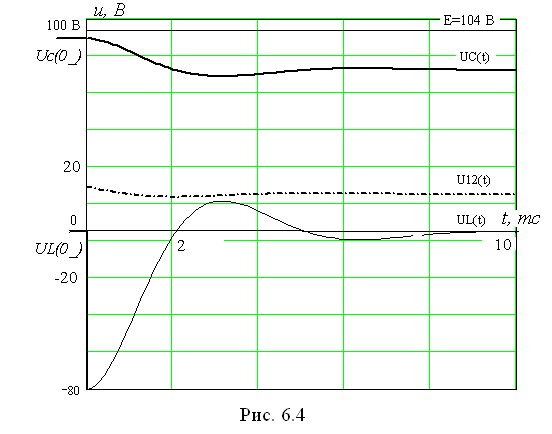
Зависимости токов от времени приведены на рис. 6.5.

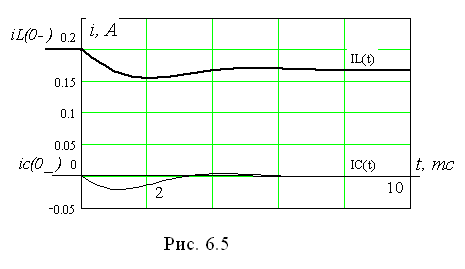
При апериодическом процессе (корни характеристического уравнения вещественные) диаграммы строятся для промежутка времени  ( - набольшая постоянная времени, получающаяся при расчете). При колебательном процессе (корни характеристического уравнения комплексные) этот промежуток составляет  (‑период колебаний).

В указанных промежутках должно быть рассчитано не менее десяти точек для апериодического процесса и не менее пятнадцати точек  для колебательного процесса. Шкалы на графиках должны быть оформлены по ГОСТ.

II. Расчет переходного процесса операторным методом

Расчет переходного процесса операторным методом производится в следующей последовательности.

II.1. Строится операторная схема замещения. Для этого необходимо:

-  мгновенные значения токов, напряжений и ЭДС заменить их изображениями по Лапласу;

-  индуктивность заменить последовательным соединением операторного сопротивления pL и добавочного источника, ЭДС которого совпадает по направлению с током  и равна ;