Домашние задания по расчету электрических цепей: Методические указания, страница 13

Примечание: Р — ключ S размыкается; 3 — ключ S замыкается.

Методические указания:

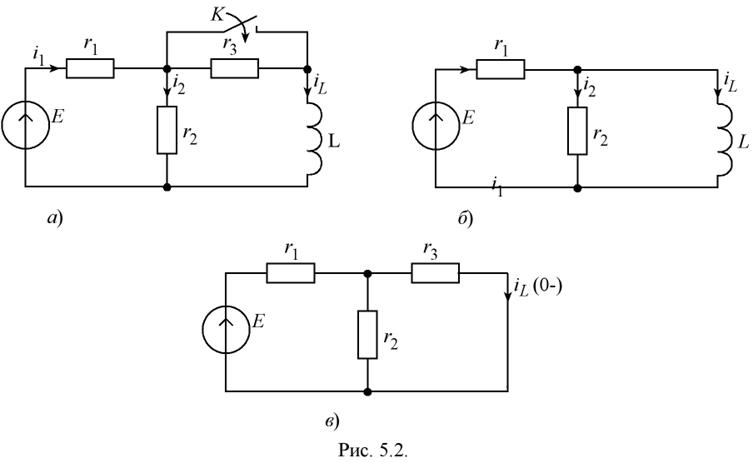
В электрической цепи, схема которой приведена на рис. 5.2, а, замыкается ключ К Требуется определить ток в индуктивности L и построить его зависимость от времени t, если параметры элементов цепи имеют следующие значения: Е = 30 В; r₁ =r₂ =r₂ = 10 Ом; L = 0,1 Гн.

1. Классический метод. Рассматривая схему цепи, приведенную на рис. 5.2 а, можно сделать следующие выводы:

1)  в схеме имеется один реактивный элемент L, поэтому дифференциальное уравнение цепи будет иметь первый порядок;

2)  при коммутации цепи сопротивление r₃ замыкается ключом К, поэтому в дальнейшем переходном процессе не участвует;

3)  переходный процесс связан с изменением энергии, запасенной в индуктивности L, при изменении структуры цепи, обусловленной замыканием сопротивления r₃.

Составим систему уравнений цепи по законам Кирхгофа, для схемы, полученной после коммутации (рис. 5.2, б):

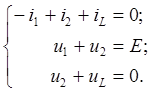
После подстановки напряжений эти уравнения приводятся к виду:

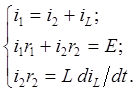
Выполнив взаимные подстановки, получим дифференциальное уравнение для тока в индуктивности

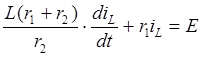
После подстановки в это уравнение значений параметров элементов, получим:

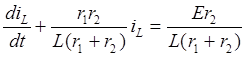или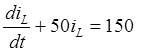

Решение этого неоднородного дифференциального уравнения состоит из двух частей:

где принужденная составляющая тока определяется в установившемся режиме после коммутации и равна (рис. 5.2 б):

Для определения свободной составляющей тока  положим правую часть дифференциального уравнения равной нулю, тогда получим:

.

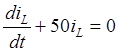Решение этого уравнения имеет вид:

Характеристическое уравнение, соответствующее дифференциальному уравнению для свободной составляющей тока, имеет вид: р + 50 = 0, откуда находим р = -50 с^-1. Модуль этой величины характеризует скорость уменьшения свободной составляющей тока и называется коэффициентом затухания. Величина, обратная коэффициенту затухания, имеет размерность времени и называется постоянной времени цепи

Таким образом, полный ток в индуктивности можно записать в виде:

При определении постоянной интегрирования А воспользуемся первым законом коммутации, согласно которому  Для вычисления тока построим схему, изображенную на рис. 5.3 в. На этой схеме индуктивность L заменена перемычкой, поэтому ток в ней рассчитаем по методу эквивалентного источника, преобразуя ветви с источником напряжения Е и сопротивлениями , , к эквивалентному  источнику с параметрами:

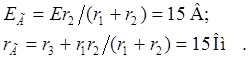
Ток в индуктивности до коммутации (т. е. при t = 0_-) определяется по формуле:

Подставив найденное значение тока  в уравнение для полного тока в индуктивности, получим:

Окончательное решение для тока в индуктивности представим в виде:

График тока в индуктивности приведен на рис. 5.3. При  значение тока  отличается от принужденного всего на 5%. Поэтому принято считать, что переходный процесс практически заканчивается через интервал времени . Из графика видно, что ток в индуктивности монотонно изменяется от начального значения 4(0) до конечного значения, равного i_Lпр= 3 А.

Располагая током в индуктивности, найдем напряжения и токи в других ветвях.

Напряжение на индуктивности определим по формуле:

График напряжения на индуктивности приведен на рис. 5.3. Из этого графика видно, что напряжение на индуктивности в результате коммутации скачком изменяется от начального значения  до значения . После этого оно монотонно убывает до значения .

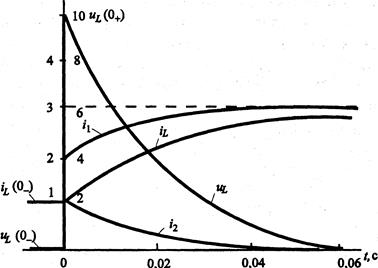
Рис. 5.3. Графики напряжения и токов в цепи.

Токи в сопртивлениях определяем по формулам:

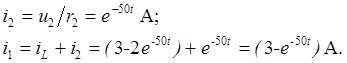
Графики токов в сопротивлениях  и  также представлены на рис. 5.3.

2.Операторный метод. В основу операторного метода расчета переходных процессов положено интегральное преобразование Лапласа:

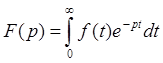, где  ‑ комплексная переменная, обычно называемая оператором,  ‑ угловая частота, с – некоторая вещественная постоянная. Применительно электрическим цепям оператор p можно рассматривать как комплексную частоту , в которой c>0 характеризует затухание гармонических колебаний, представленных вращающимся вектором .