Домашние задания по расчету электрических цепей: Методические указания, страница 4

В цепи, представленной на рис 1.1 (см. задание 1), действуют два (из пяти возможных) источника синусоидальной ЭДС , . Модули сопротивлений элементов цепи:  при частоте . Начальная фаза ЭДС  и характер сопротивлений заданы в таблице 1.1. Нумерация сопротивлений таблицы 1.1 приведена в таблице 1.2 (см. задание 1).

Номер варианта задает преподаватель в виде четырех чисел, например 25 ‑7 ‑ 2 ‑ 3 . Первое число указывает на номер строки в табл. 1, второе число определяет нумерацию сопротивлений (табл. 1) в соответствии с номером строки в таблице 2, третье и четвертое числа указывают номера сопротивлений, последовательно с которыми включены источники и . Указанный вариант означает, что , , , , , , , источник ЭДС включен последовательно с сопротивлением , а источник  ‑ последовательно с сопротивлением .

Требуется:

1.  Составить и решить на компьютере систему алгебраических уравнений в комплексной форме:

1.1  по законам Кирхгофа;

1.2  по методу контурных токов.

2.  Значения токов в ветвях и напряжения на всех участках, найденные с помощью законов Кирхгофа, записать в алгебраической и показательной формах. Перейти от комплексов токов и напряжений к их мгновенным значениям. Комплексы действующих контурных токов привести в алгебраической и показательной формах.

3.  Найти комплексы действующих значений токов в ветвях в алгебраической и показательной формах. Сравнить результаты, полученные двумя способами.

4.  Составить и решить систему алгебраических уравнений в комплексной форме методом узловых потенциалов. Определить токи в ветвях. Сравнить полученные значения токов со значениями, полученными в п.1.

5.  Проверить баланс активных мощностей.

6.  Определить показания амперметра, вольтметра и ваттметра.

7.  Построить векторные диаграммы токов и напряжений.

8.  Определить ток в одной из ветвей цепи, не содержащей источника ЭДС, методом эквивалентного генератора (ЭДС эквивалентного генератора найти методом наложения). Сравнить полученное значение тока с его значением, найденным по законам Кирхгофа и  методом комплексных токов.

9.  Определить сопротивление каждого элемента при изменении частоты в n раз (n задано в табл. 1.1).

Методические указания.

Рассмотрим последовательность выполнения задания на примере варианта 30 –13 –1 ‑3. Изображение каждого элемента должно соответствовать его характеру (R,L или С). В соответствии с указанным вариантом, исходная схема показана на рис. 2.1. Комплексные сопротивления элементов имеют значения :Z₁=j10Oм, Z₂=-j30Oм, Z₃=40Ом, Z₅₌60 Ом, комплексы действующих ЭДС Е₁=100В, Е₂₌127е^j25В.

1.  Составление системы уравнений по законам Кирхгофа в комплексной форме:

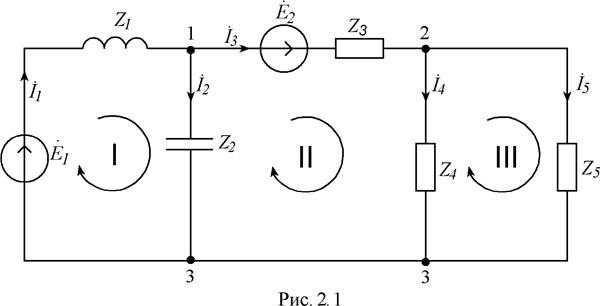
Выбираем направления токов в ветвях и направления обхода контуров. Составим систему уравнений для комплексов действующих токов и напряжений:

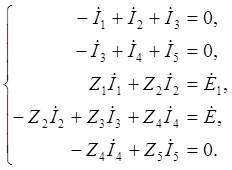                                                                     (2.1)

Подставляем данные элементов и запишем систему уравнений (2.1) в матричной форме :

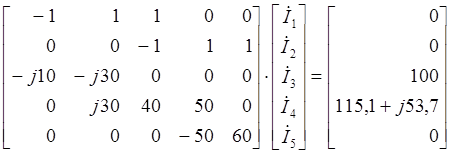,                                       (2.2)

где квадратная матрица A – обобщенная матрица коэффициентов, I – вектор токов ветвей, E - столбец правой части – вектор входных воздействий.

Систему уравнений (2.2) решаем с помощью программы MathCAD (пример решения в приложении №2) и находим комплексные амплитуды токов в элементах схемы.

Далее, используя закон Ома в комплексной форме, определяем комплексные амплитуды напряжений на элементах схемы.

Записываем все токи и напряжения в алгебраической и показательной формах.

Используя значения комплексных амплитуд, записываем их мгновенные значения.

Результаты вычислений оформляем в виде таблицы.

Ток	Форма записи токов
	Арифметическая	Показательная	Тригонометрическая	Мгновенные значения

2. Составление системы уравнений по методу контурных токов.

Выбираем направления контурных токов I_кi, совпадающие с обходом контуров на схеме рис 2.1. Далее, составляем систему уравнений для рассматриваемой схемы: