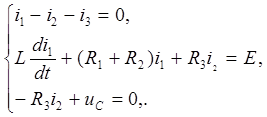Домашние задания по расчету электрических цепей: Методические указания, страница 16

                                                (6.1)

и уравнение связи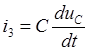                   

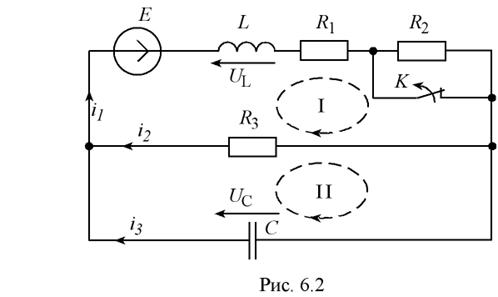
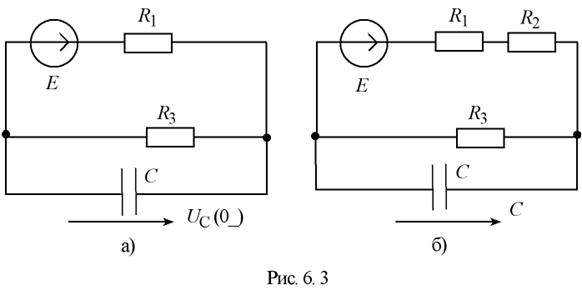
1.2. Определение независимых и зависимых начальных значений, напряжений и токов в схеме в момент времени (Рис. 6.3,а):

I.2.1 Независимые  начальные условия определяются количеством реактивных накопителей энергии в схеме. Состояние каждого накопителя может быть охарактеризовано либо текущим через него током, либо падением напряжения на нем. Независимыми переменными являются: для емкости – напряжение на ней, для индуктивности – ток через нее.

Согласно первому закону коммутации ток через индуктивность непосредственно до коммутации  равен току через ту же индуктивность после коммутации . Ток через индуктивность L (рис. 6.3,а) до коммутации имел значение:

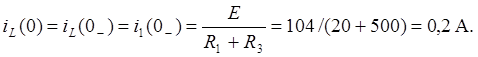                             (6.2)

Ток в емкости до коммутации отсутствовал, поэтому .

Напряжение на индуктивности также отсутствовало, поэтому .

Согласно второму закону коммутации, напряжение на емкости до коммутации равно напряжению непосредственно после коммутации. Напряжение до коммутации было равно падению напряжения на резисторе R₃, включенным параллельно ей:

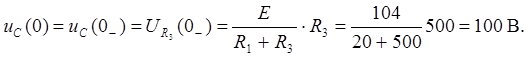                    (6.3)

I.2.2. Зависимые начальные условия. Значения остальных токов и напряжений при  в послекоммутационной схеме (рис 6.2), определяемые по независимым начальным значениям  из законов Кирхгофа называются зависимыми начальными условиями. Составим систему уравнений для определения зависимых начальных условий:

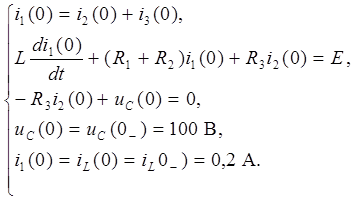                        (6.4)

Подставляя данные схемы, получаем:

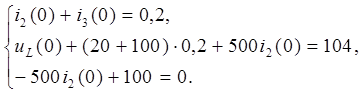                       (6.5)

Решая систему уравнений (6.5) находим зависимые начальные условия:

; ; .                         (6.6)

I.3. Система уравнений (6.1) сводится к одному дифференциальному уравнению второго порядка относительно напряжения . (Если систему уравнений (6.1) сводить к одному уравнению относительно тока , то получиться не дифференциальное уравнения, а интегро-дифференциальное уравнение). Для этого из третьего и первого уравнений системы (6.1):

 ,                                                                    (6.7)

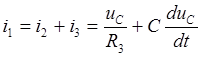.                                                           (6.8)

Дифференцируя (6.7) и подставляя результат во второе уравнение системы (6.1), получим

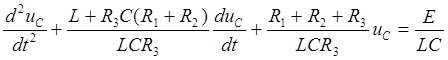.                             (6.9)

Получено линейное неоднородное дифференциальное уравнение второго порядка. Известно, что решением таких уравнений является сумма двух составляющих, а именно, общего решения  для соответствующего однородного уравнения и частного решения, полученного в форме правой части для неоднородного уравнения. Физический смысл первой составляющей – описание поведения системы при отсутствии внешнего воздействия. Эту составляющую принято называть свободной составляющей (далее обозначено ). Физический смысл второй составляющей – описание поведения системы при наличии внешнего воздействия, описываемого правой частью неоднородного уравнения. Эту составляющую принято называть принужденной составляющей (далее обозначена u_Cпр). По существу, это описание нового установившегося процесса, в которой должна будет перейти система после коммутации.

Таким образом, решение уравнения (6.9)

 .                                                               (6.10)

Принужденная составляющая напряжения u_C определяется в установившемся режиме после коммутации и равна (рис.6.3, б)

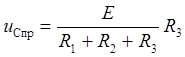.                                                            (6.11)

Свободная составляющая напряжения  определяется решением однородного дифференциального уравнения

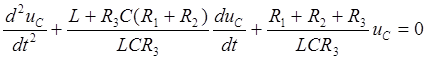.                         (6.12)

Решение однородного дифференциального уравнения (6.12) позволяет найти свободную составляющую напряжения

                                                              (6.13)