3. Расчет электрической схемы методом эквивалентных преобразований.
С помощью метода эквивалентных преобразований находим эквивалентное (входное) сопротивление цепи. Будем определять сопротивления участков цепи (используем составные индексы, состоящие из индексов участвующих элементов). При этом все результаты целесообразно записывать и в показательной и алгебраической формах, поскольку для умножения и деления удобнее показательная, а для суммирования и вычитания – алгебраическая форма.
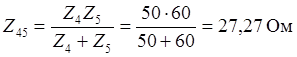
![]()
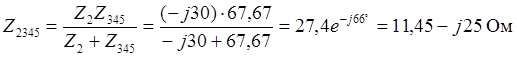
![]() .
.
По закону Ома
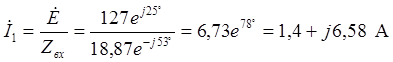 .
.
Тогда ![]() .
.
Дальнейшие шаги расчета можно проводить двумя способами: по закону Ома или законам Кирхгофа. Можно пользоваться любым методом, а можно пользоваться и обеими одновременно, что позволит сравнивать результаты с целью текущей самопроверки.
По законам Кирхгофа
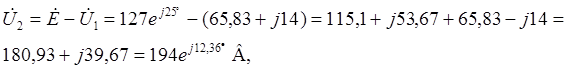
по закону Ома ![]()
(незначительные отклонения допустимы, поскольку расчет производился с округлением результата после каждого шага).
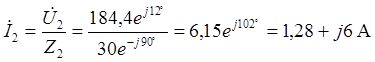
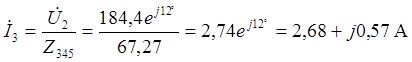 , или
, или ![]()
![]()
![]()
или ![]()
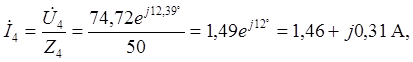
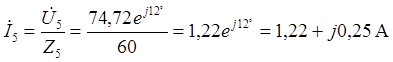
или ![]() . Рассчитанным выше
значениям комплексов токов и напряжений соответствуют следующие мгновенные
значения величин:
. Рассчитанным выше
значениям комплексов токов и напряжений соответствуют следующие мгновенные
значения величин:
![]() ,
,
![]() В,
В,
![]() ,
,
![]() В,
В,
![]() ,
,
![]() В,
В,
![]() ,
,
![]() В,
В,
![]() ,
,
![]() В.
В.
Полученные методом эквивалентных преобразований значения токов сравниваем с результатами расчета с помощью прикладной программы MathCAD.
4. Проверка баланса активных и реактивных мощностей.
Проверка баланса мощностей проводится в соответствии с уравнением
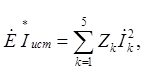
где ![]() – сопряженный комплекс
тока ветви, в которую включен источник,
– сопряженный комплекс
тока ветви, в которую включен источник, ![]() -
комплексное напряжение источника,
-
комплексное напряжение источника, ![]() – комплекс сопротивления
и действующий ток ветви
– комплекс сопротивления
и действующий ток ветви ![]() .
.
Для рассмотренного варианта:
![]() .
.
Определяем полную мощность источника:
![]() .
.
Далее определяем полную мощность приемников цепи:
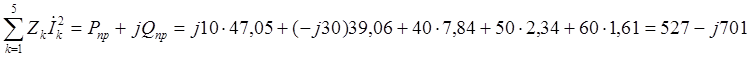
Проводим оценку баланса по формулам
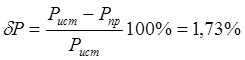 ;
;
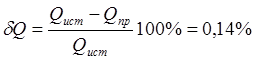 .
.
Полученное расхождение находится в пределах погрешности вычислений.
5. Определение показаний приборов.
Амперметр показывает действующее значение тока IA=I2= 6,25 А. Вольтметр – действующее напряжения Uv = U4 = 76.5 В.
Показание ваттметра определяется произведением действующих значений измеряемого напряжения и измеряемого тока, умноженным на косинус сдвига фаз между ними:
![]() Вт.
Вт.
6. Построение векторной диаграммы токов и напряжений.
Для построения векторной диаграммы (рис 1.3) можно воспользоваться любой из форм представления комплексов действующих значений токов и напряжений.
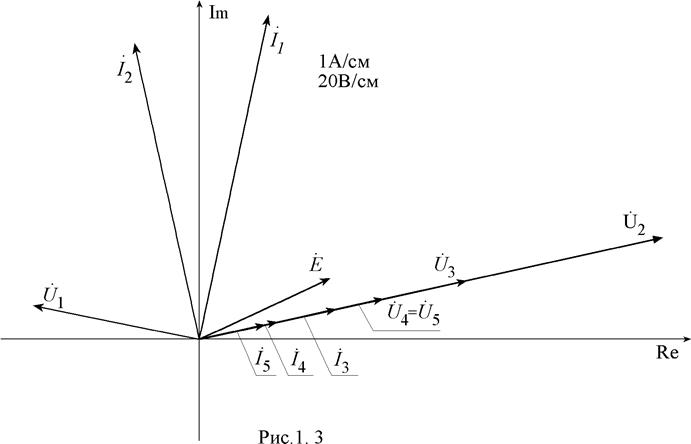 |
Векторная диаграмма строится, на миллиметровке с использованием масштабов, соответствующих ГОСТ. Желательно выделять токи и напряжения разными цветами. Заметим, что пользуясь правилами сложения векторов, можно по векторной диаграмме легко проверить выполнение уравнений (1.1), составленных по законам Кирхгофа при подстановке в них рассчитанных выше результатов.
7. Определение сопротивления каждого элемента при изменении частоты в n раз проводим с учетом зависимостей индуктивного и емкостного сопротивлений от частоты.
8. Определение тока в одной из ветвей методом эквивалентного генератора (Э.Г.).
Номер ветви, ток в которой следует определить методом Э.Г., задается преподавателем. Определение тока методом Э.Г. произведем на примере второй ветви схемы по тому же (рассмотренному выше) варианту 30-13-1.
В соответствии
с сущностью метода, схема Э.Г. имеет вид, приведенный на рис. 1.4.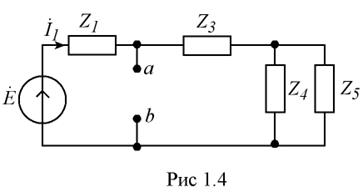
В этой схеме интересующая нас нагрузка присоединяется к точкам a и b. Пользуясь
результатами, полученными выше, имеем ![]() Ом.
Тогда внутреннее сопротивление источника Э.Г., определяемого между точками a и b при замене
источника Е его внутренним сопротивлением будет:
Ом.
Тогда внутреннее сопротивление источника Э.Г., определяемого между точками a и b при замене
источника Е его внутренним сопротивлением будет:
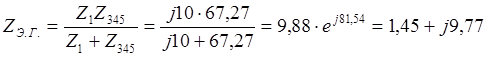 Ом.
Ом.
ЭДС Э.Г.
отличается от ЭДС источника Е на величину падения напряжения,
создаваемого током I, на сопротивлении ![]() .
.
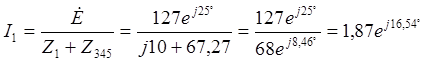 А,
А,
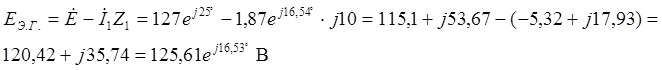
Искомый ток определяется в соответствии со схемой на рис 1.5
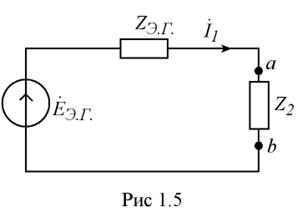
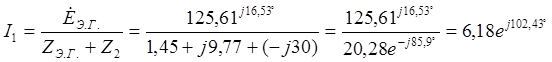 А.
А.
Сравнение этого результата с результатом, полученным ранее, дает расхождение, приемлемое в пределах погрешности вычислений.
Задание 2. РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА РАЗЛИЧНЫМИ МЕТОДАМИ
Исходные данные:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.