ПЕРЕДМОВА
Навчальна дисципліна “Теорія автоматичного керування” має велике значення у підготовці фахівців зі спеціальності 7.092203 “Електромеханічні системи автоматизації та електропривод” тому, що вона є теоретичною основою, на якій ґрунтується ряд спеціальних дисциплін навчального плану спеціальності: теорія електроприводу, системи керування електроприводами, автоматизований електропривод типових виробничих механізмів та інші.
Лекційна частина курсу доповнюється практичними та лабораторними заняттями.
Метою практичних занять з дисципліни “Теорія автоматичного керування” є закріплення та розширення знань, що одержані студентами на лекціях, а також під час самостійної роботи з літературою.
Головне завдання практичних занять – це набуття студентами навичок проведення розрахунків і вирішення конкретних задач з використанням методів теорії автоматичного керування.
У методичних вказівках розміщені задачі з усіх розділів (модулів) дисципліни “Теорія автоматичного керування“, у яких використані джерела з теорії керування, а також матеріал із фахових дисциплін ( теоретичних основ електротехніки, електричних машин і теорії електропривода ), де здебільшого знаходять застосування методи теорії автоматичного керування. На практичних заняттях широко використовуються також методи рішення диференційних рівнянь, методи теорії операційного та варіаційного обчислювання, теорії імовірності, ряди та інші, тому що теорія автоматичного керування є необхідною ланкою в ланцюзі, що забезпечує неперервність математичної підготовки студентів.
1 ПРИНЦИПИ АВТОМАТИЧНОГО КЕРУВАННЯ ТА
МАТЕМАТИЧНІ МОДЕЛІ ЛІНІЙНИХ БЕЗПЕРЕРВНИХ
СИСТЕМ АВТОМАТИЧНОГО КЕРУВАННЯ (САК)
(МОДУЛЬ 1)
1.1 Практичне заняття 1.
Принципи автоматичного керування та типи САК
по задачам керування
Методичні вказівки
Головними принципами керування є принцип розімкненого керування, принцип компенсації (запропонований Понселе в 1829р. ), принцип зворотного зв’язку .
Також може бути спільне (комбіноване) використання принципів керування, наприклад, принципу компенсації збурення та принципу зворотного зв’язку.
По задачам керування системи розподіляються на: системи стабілізації, системи програмного керування, слідкуючи системи.
При підготовці до цього практичного заняття рекомендується використати матеріал: [1] – c.5-16; [2] – c. 17-28; [9] – c.25-35, а також конспект лекцій.
1.1.1. Показати що подільник напруги може бути прикладом, як розімкненої, так і замкненої системи керування. Електрична схема подільника напруги наведена на рисунок 1.1. Вважати вхідним сигналом напругу U1, вихідною координатою – U2.
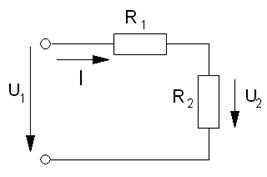
Рисунок 1.1- Електрична схема подільника напруги
Розв’язання
а) холостий хід (х.х.)
По закону Ома
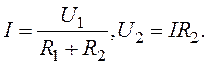
Отже
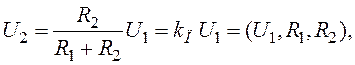
де kП – коефіцієнт передачі (підсилення) подільника.
Напруга U2 під знак функції не входить, що є ознакою розімкненої системи.
Структурна схема подільника напруги для режиму х.х. має вигляд

Рисунок 1.2 - Структурна схема подільника напруги
для режиму холостого ходу
б) режим навантаження
По закону Ома
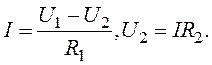
Отже
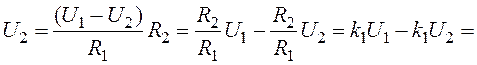
![]()
де
k1 – коефіцієнт підсилення подільника;
ΔU – похибка.
Напруга U2 в цьому разі входить під знак функції f2, що є ознакою замкненої системи.
Структурна схема подільника для режиму навантаження наведена на рисунку 1.3
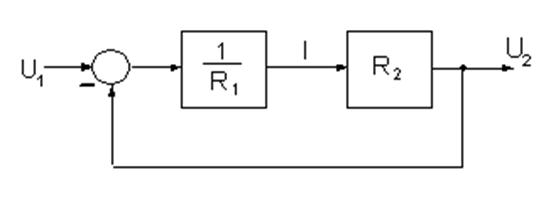
Рисунок 1.3 - Структурна схема подільника напруги
для режиму навантаження
1.1.2 Зобразити функціональну схему системи автоматичного керування двигуном постійного струму незалежного збудження з сумуючим підсилювачем, якого підключено до обмотки незалежного збудження генератора (система Г-Д), з від’ємними зворотними зв’язками за швидкістю і струмом. Вважати вихідною величиною швидкість двигуна ω, а керуючою і збурюючою діями – напругу керування Uk і статичну складову струму Ic .
1.1.3 Скласти функціональну схему слідкуючої системи, принципова схема якої наведена на рисунку 1.4
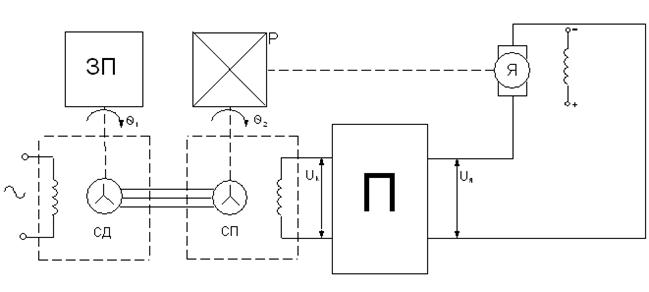
Рисунок 1.4 ‑ Принципова схема слідкуючої системи
Принципова схема, яка зображена на рисунку 1.4, має в собі пристрій що задає кут ЗП, сельсин-давач СД, сельсин-приймач СП, фазочутливий перетворювач П, якір двигуна постійного струму незалежного збудження Я, редуктор Р.
Сельсини СД і СП працюють в трансформаторному режимі і виконують функції вимірювача розузгодження вхідного і вихідного кута θ1 і вхідного θ2. Поясніть принцип роботи слідкуючої системи.
1.1.4 Показати, що електродвигун постійного струму незалежного збудження, як об’єкт керування в замкненій системі, в той же час по принципу його роботи є також замкненою системою (доказ здійснити для статичного режиму).
1.1.5 Якою повинна бути система керування по задачам керування, щоб забезпечити виконання наступних технологічних операцій:
забезпечити потрібний закон нагрівання підкладок мікросхем;
‑ дистанційно переміщувати робота – маніпулятора;
‑ підтримувати постійну температуру в приміщенні.
1.2 Практичне заняття 2.
Математичні моделі динамічних ланок і САК.
Диференціальні рівняння
Методичні вказівки
В теорії автоматичного керування для аналізу і синтезу систем використовують різні математичні моделі динамічних ланок і САК:
- диференціальні рівняння;
- передатні функції;
- комплексні передатні функції(частотні характеристики);
- структурні алгоритмічні схеми.
Диференціальні рівняння – основна математична модель динамічних ланок і систем.
Існує дві форми запису диференціальних рівнянь: форма ВВ (вхід-вихід) для реальних вхідних і вихідних змінних динамічних ланок і САК, а також форма ЗC (змінних стану) для абстрактних вихідних змінних (форма Коши)[2].
Записуючи диференціальні рівняння у формі ВВ (це стосуються також і передатних функцій), треба мати на увазі такі умовності [10]:
1) в лівій частині рівняння мають бути керована (вихідна) координата зі своїми похідними, в правій – зовнішні сигнали (завдання та збурення);
2) члени кожної змінної розташовуються у порядку зменшення похідної;
3) бажано, щоб коефіцієнти при щонайменших похідних дорівнювали одиниці.
Відзначимо також, що у результаті розв’язання, тим чи іншим методом, диференціального рівняння одержуємо часові характеристики типових ланок і систем: перехідні функції, які є реакцією на одиничний стрибок, та імпульсні перехідні функції (функції ваги) – реакції на одиничний імпульс.
Часові характеристики (перехідні та функції ваги) використовують для аналізу якості та стійкості автоматичних систем.
При підготовці до розв’язання задач цього підрозділу рекомендується використати матеріал: [1] – c.53-69; c. 99-100; c. 126-138; [2] – c.50-58; c.75-86; [9] – c.36-49, а також конспект лекцій.
1.2.1 Скласти диференціальні рівняння двигуна постійного струму незалежного збудження і записати їх у формах ВВ та ЗС. Вважати що x0(t)=Uя(t); f(t)=Mc(t)=const; x(t)=ω(t); Uз(напруга збудження)=const.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.