1.4 Практичне заняття 4
Математичні моделі динамічних ланок і САК.
Структурні схеми. Перетворення і складання структурних схем
Методичні вказівки
Під структурною схемою розуміють графічне зображення математичної моделі системи у вигляді передатних функцій з показом зв’язків між ними. Кожна ланка структурної схеми зображається прямокутником, в якому відображуються у вигляді передатних функцій динамічні властивості даної ланки. Інколи у прямокутнику відображають рівняння динаміки або часові характеристики. Вхідні і вихідні величини на структурних схемах можуть бути записані у вигляді зображень або їх оригіналів.
Ланки, які забезпечують підсумування (алгебраїчне деяких величин, зображують у вигляді кола).
Якщо вхідні величини мають різний знак, то це відображується знаком „мінус” у стрілки біля кола.
Структурні схеми широко застосовують в теорії автоматичного керування при дослідженнях і проектуванні систем. По структурним схемам легко простежуються зв’язки між ланкою, їх вплив, а також проходження сигналів у системі.
По структурній схемі можна безпосередньо провести моделювання автоматичної системи.
Якщо з’явиться необхідність скласти диференціальне рівняння заданої САК по її структурній схемі, то останню потрібно перетворити.
Перетворення структурної схеми виконують для її спрощення, зведення до одноконтурної, після чого вже зручно складати диференціальне рівняння САК.
Для перетворення структурних схем при наявності перехрещування зворотних зв’язків необхідно знати правила перетворення і вміти користуватись ними.
При перетворенні структурних схем використовуйте найпростіші правила. Перенесення вузла через суматор або суматора через вузол використовуйте тільки в крайніх випадках.
До вузла і суматора, які розташовані поруч, треба підходити дуже обачливо, бо в цьому випадку у ланцюг зворотного зв’язку треба вводити фіктивну ланку, передатна функція якої є співвідношенням певних передатних функцій. Недопустимо просто (без правил) міняти місцями суматор і вузол.
Для вирішення задач цього підрозділу рекомендується використати матеріал: [1] – c. 116-126; [2] – c. 129-146; [3] – c. 26-30, табл. A5-A6; [4] – c. 32-36; [9] – c. 109-137; [10] – c. 10-18.
1.4.1 Записати еквівалентні передатні функції системи, структурна схема, якої наведена на рисунку 1.13
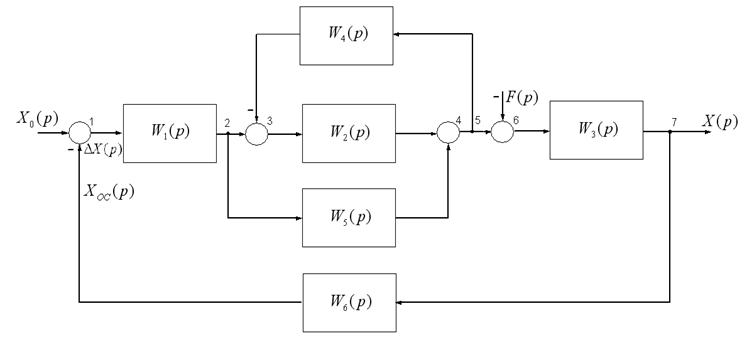
Рисунок 1.13 ‑ Структурна схема системи автоматичного керування.
Розв’язання.
При перетворенні багатоконтурної алгоритмічної структурної схеми рекомендується виконувати перетворення в такій послідовності:
‑ліквідація явища перехрещування зворотних зв’язків;
‑об’єднання суматорів та вузлів;
‑заміна типових з’єднань еквівалентними в такій, наприклад, черзі: паралельних, послідовних, із зворотним зв’язком (зустрічно-паралельних).
Ознакою перехрещування зворотних зв’язків є те, що зворотний зв’язок охоплює групу ланок, які мають тільки початок, або тільки кінець другої ланки зворотного зв’язку.
На рисунку 1.14 перехрещування зв’язків має місце між
елементами з передатними функціями ![]() . Ліквідувати
явище перехрещування можна двома шляхами.
. Ліквідувати
явище перехрещування можна двома шляхами.
Перший шлях – це перенести суматор 4 паралельного зв’язку
через ланку з ![]() і об’єднати з суматором 3,
або суматор 3 зворотного зв’язку через ланку
і об’єднати з суматором 3,
або суматор 3 зворотного зв’язку через ланку ![]() і
об’єднати з суматором 4.
і
об’єднати з суматором 4.
При об’єднанні суматорів 4 і 3 у ланцюг паралельного
зв’язку вводиться фіктивна ланка з 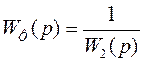 , а при
об’єднанні суматорів 3 і 4 у ланцюг зворотного зв’язку вводиться фіктивна ланка
з
, а при
об’єднанні суматорів 3 і 4 у ланцюг зворотного зв’язку вводиться фіктивна ланка
з ![]() (дивись відповідно рисунку 1.14
та рисунку 1.15)
(дивись відповідно рисунку 1.14
та рисунку 1.15)
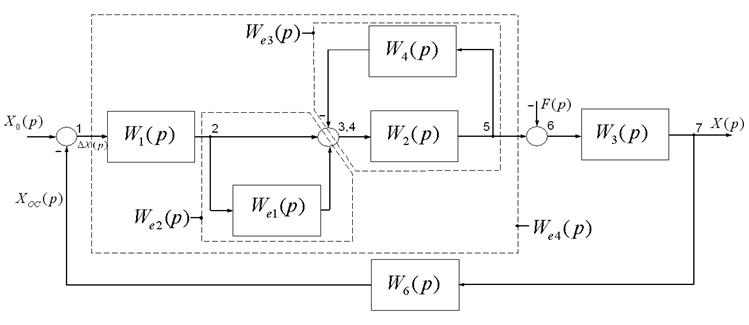
Рисунок 1.14 ‑ Перетворена структурна схема
На ньому:
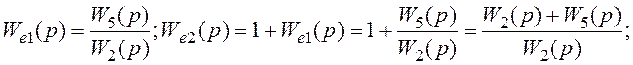
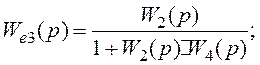
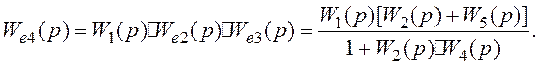
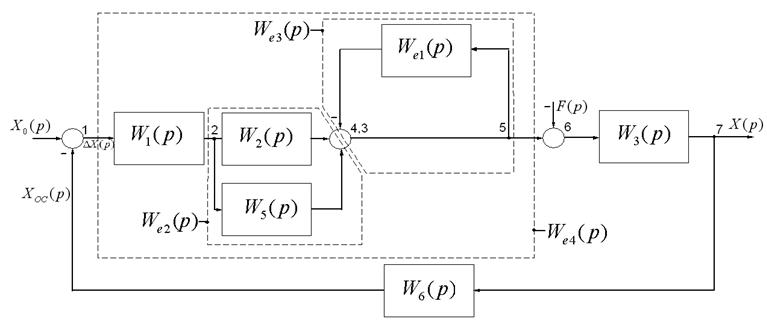
Рисунок 1.15 ‑ Перетворена структурна схема
На ньому:
![]()
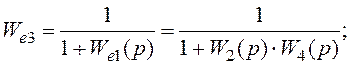
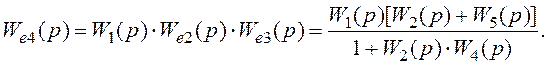
Вирази (1.55) і (1.56) – тотожні.
Ураховуючи (1.55), чи (1.56), одержуємо одноконтурну структурну схему, яка наведена на рисунку 1.16.
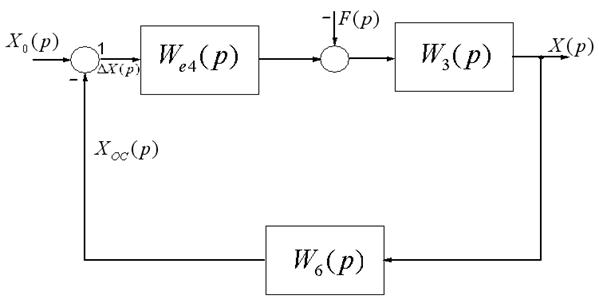
Рисунок 1.16 ‑Перетворена структурна схема
Далі перетворювати структурну схему нема сенсу, тому що з неї безпосередньо записуємо всі необхідні передатні функції системи:
‑головну передану функцію
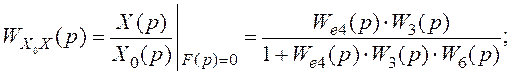
‑ передатну функцію по збуренню
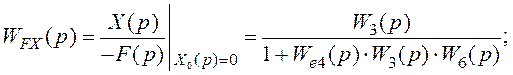
‑ передатну функцію по похибці від змінювання задавального діяння
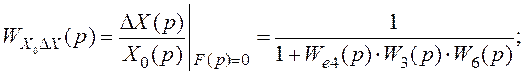
‑ передатну функцію розімкненої системи
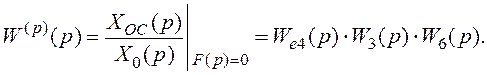
Вираз для вихідної координати матиме вигляд:
![]()
Чи
![]()
![]()
Другий шлях – це перенести вузол 5 через суматор 4 чи вузол 2 через суматор 3.
Розглянемо перший варіант – перенесення вузла 5 через суматор 4.
Структурна схема у відповідності до цього варіанту наведена
на рисуку1.17.
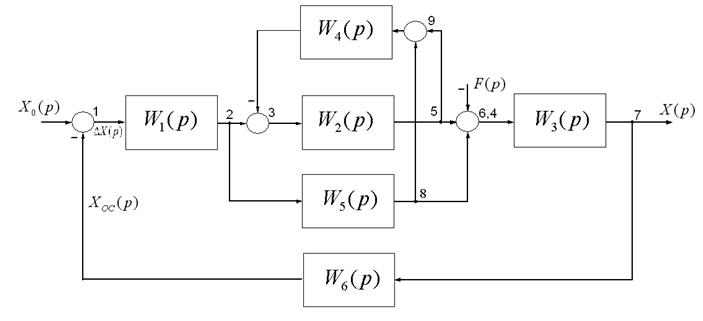
Рисунок 1.17 ‑Перетворена структурна схема
Далі слід перенести суматор 9 через ланку з ![]() і об’єднати з суматором 3, а вузол 8
через ланку
і об’єднати з суматором 3, а вузол 8
через ланку ![]() і об’єднати з вузлом 2.
і об’єднати з вузлом 2.
Схема, що відповідає зробленим перетворенням, наведена
на рисунку1.18.
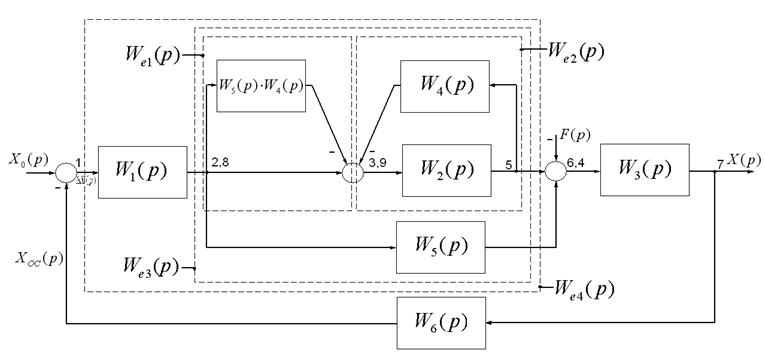
Рисунок 1.18 ‑Перетворена структурна схема
На ньому:
![]()
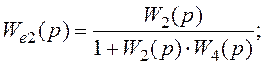
![]()
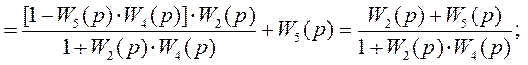
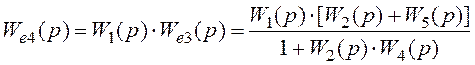
Перший і другий шляхи ліквідації явища перехрещення приводять до одного і того же результату.
Вирази (1.55), (1.56), (1.63) – тотожні, але другий шлях вимагає більше часу на перетворення.
1.4.2. Докажіть, що між структурними схемами, наведеними на рисунку 1.9 та рисунку 1.10, двигуна постійного струму з незалежним збудженням можна поставити знак тотожності.
1.4.3 По операторно му рівнянню динамічних ланок системи запишіть передатні функції ланок і складіть структурну схему. Із структурної схеми отримайте головну передатну функцію системи і запишіть диференціальне рівняння системи. Назвіть типи динамічних ланок, що входять в структурну схему
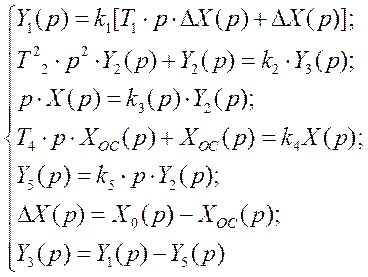
1.4.4 Зробіть перетворення структурної схеми, наведеній на рис. 1.13, за умови, що ліквідація явища перехрещування зворотних зв’язків здійснюється за рахунок перенесення вузла 2 через суматор 3 і запишіть передатну функцію по збуренню якщо:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.