Принципи автоматичного керування та математичні моделі лінійних безперервних систем автоматичного керування, страница 10

Критичне значення коефіцієнта підсилення визначають по формулам:

                                        ,                                               (2.31)

                                                                                         (2.32)

Із (2.32) вишукують  використовуючи вираз

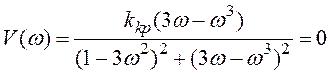                                                  (2.33)

або                  

                                                                               (2.34)

Із виразу (2.24) при  маємо

                                                                                    (2.35)

Отже.

Далі визначають, використовуючи вираз

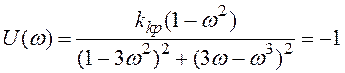                                              (2.36)

або

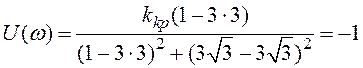                         .                  (2.37)

Деякі перетворення виразу (2.37) приводять до числового значення

2.1.2 Інерційна ланка охоплена негативним зворотним зв’язком з запізненням на час τ. Структурна схема замкненої системи наведена на рисунку 2.4

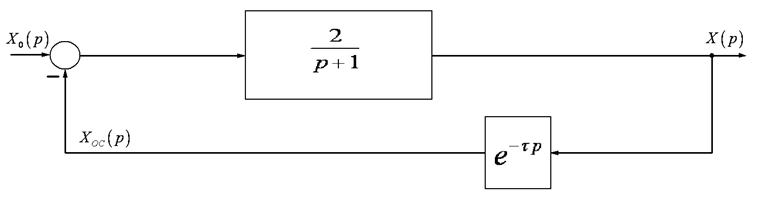
                                Рисунок 2.4 -‑Структурна схема

Треба вияснити, при якому значенні   замкнена система стає нестійкою.

Розв’язання

Характеристичний поліном замкненої системи визначається з передатної функції, яка має вигляд

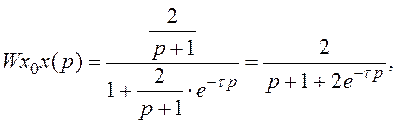                                        (2.38)

         де характерний поліном замкненої системи

                                           ,                                       (2.39)

Як відзначалось раніше критерії Гурвіца та Рауса є неприйнятними для розв’язання цієї задачі. Найбільш прийнятним є використання у цьому випадку критерію Найквіста.

Розглянемо критичний випадок – проходження годографа Найквіста через точку с координатами [-1, jo].

Визначаємо модуль

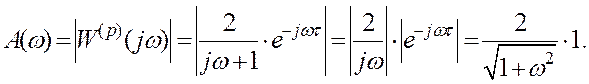                (2.40)

При  

тобто 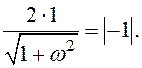                                                                          (2.41)

З виразу (2.41) одержуємо 

Далі записуємо вираз для кута при

                                                 (2.40)

Деякі перетворення (2.42) приводять до числового значення

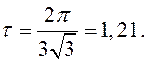                                                                                   (2.41)

Таким чином при значенні  замкнена система стає нестійкою.

2.1.3 Покажіть, що в замкненій системі, яка складається з “n” однакових інерційних ланок першого порядку з  критичне за умовами стійкості значення загального передатного коефіцієнта розімкненого контура не залежить від сталих часу Т та дорівнює

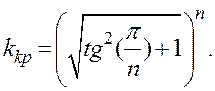
2.1.4 Покажіть, чи може розімкнена нестійка система з передатковою функцією

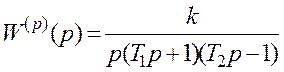                                                          (2.44)

бути стійкою в замкненому стані. Якщо це принципово неможливо, то чому?

2.1.5 Передатна функція розімкненої системи

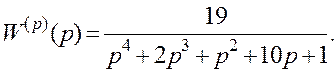                                                   (2.45)

Докажіть, що в замкненому стані система буде мати два правих полюси.

2.1.6 Докажіть, що лінійна неперервна замкнена система з характеристичним рівнянням

                                         (2.46)

  по наслідку критерію Михайлова стійка.

2.1.7 Докажіть, що критичний коефіцієнт підсилення  в лінійній неперервній одно контурній системі керування, якщо передатна функція розімкненої системи

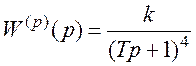                                                                          (2.47)

Покажіть практичні шляхи підвищення коефіцієнта

2.1.8 Дослідити стійкість системи автоматичного керування з характеристичним рівнянням

                                              (2.48)

за методом D – розбиття відносно коефіцієнта підсилення розімкненої систем.

2.1.9 Передатна функція розімкненої системи.

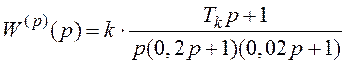                                                            (2.49)

Визначте діапазон значень сталої часу корегуючої ланки, за яких замкнена система стійка при всіх додатних значеннях добротності за швидкістю k.

2.1.10 Визначте критичне значення часу запізнення τ для системи з запізненням, якщо передатна функція розімкненої системи

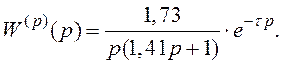                                                             (2.50)

2.1.11 Задана система з астатизмом третього порядку. Послідовно з інтегруючими ланками (у яких k=1) включені пропорційна і дві форсуючих ланки з коефіцієнтами підсилення і  і сталими часу і  відповідно;;

Визначити, при яких значеннях  замкнута САК стійка, якщо

2.1.12 За яких значень сталої часу Т замкнена система стійка, якщо передатна функція розімкненої САК

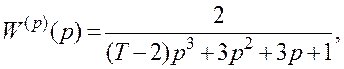
а коефіцієнт давача зворотного зв’язку – пропорційна ланка з

2.1.13 Визначити невідомий параметр  за умовою стійкості замкненої системи, якщо передатна функція розімкненої має вигляд

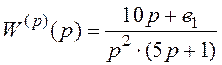                                                                    (2.50)

2.1.14 Визначити умови стійкості замкненої САК, передаткова функція якої в розімкненому стані має вигляд

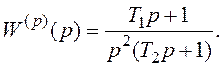                                                                  (2.52)

Підтвердити свої висновки за допомогою ЛАЧХ і ЛФЧХ.

3  ЯКІСТЬ  ЛІНІЙНИХ НЕПЕРВНИХ САК

(МОДУЛЬ 3)

3.1 Практичні заняття 9 і 10

Методичні вказівки

Якість системи оцінюється багатьма показниками, серед яких основними є: характер перехідного процесу, тривалість перехідного процесу, пере регулювання, точність (похибка) системи.

За характером перехідні процеси поділяються на монотонні, коливальні й аперіодичні з пере регулюванням.

Точність САР є одним із найважливіших показників якості систем. Точність роботи САР в її типових режимах залежить від відповідних передаткових функцій, зовнішніх збурень і заданих сигналів.

Типовими режимами роботи САР є:

‑ статичний режим, при якому всі зовнішні дії на систему і всі координати системи не змінюються;

‑-  усталений динамічний режим, при якому зовнішні дії на систему змінюються за деяким законом;

‑ перехідний динамічний режим, який має місце при переході системи від одного усталеного режиму, включаючи статичний, до іншого.