Принципи автоматичного керування та математичні моделі лінійних безперервних систем автоматичного керування, страница 7

Залежно від вигляду R(p) ланка може реагувати: на саму величину; тільки на похідну від вхідної величини; на інтеграл від вхідної величини; на вхідну величину та її похідну; на вхідну величину та інтеграл від неї; на вхідну величину, похідну та інтеграл від неї; та на інші варіанти вхідних дій.

Крім типових ланок в системі іноді зустрічаються особливі ланки: трансцендентні, ірраціональні, немінімально-фазові та інші, особливості та характеристики яких також треба знати.

Для вирішення задач цього підрозділу рекомендується використати матеріал: [1]-с.60-77; [2]-с.55-58, 65-69, 92-122; [3]-с.17-24;[4]-с.20-24, 37-51;[9]-с.72-108;[10]-с.19-24; [11]-с.35-45.

1.6.1 Побутувати часову характеристику h(t) інтегруючої ланки з сповільненням, передатна функція якої має вигляд

                                                    

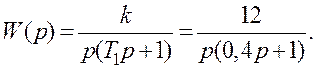
Розв’язання

Згідно з (1.95)

                                                          

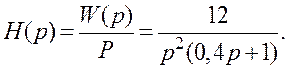
Для визначення h(t) використаємо [3]-табл.А2 відповідності зображень Лапласа оригіналам.

В таблиці А2 відсутня функція F(p), що відповідає виразу (1.97). Тоді зробить перетворення Н(p) на прості дроби, записуючі вираз (1.97) у вигляді

                    .         

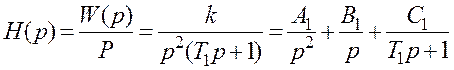Після знаходження,і  маємо

                              

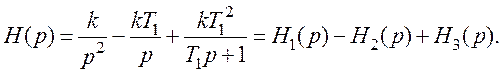
Згідно з таблиці А2

                                                                 

                                                                

              

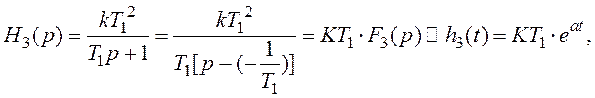
          де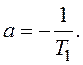

Отже, підсумкова перехідна функція

                       

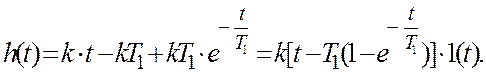
або

                                                           

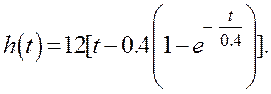
Змінюючи t від 0 до, тобто від 0 до 1,6 С, будуємо h(t).

Підсумкова перехідна функція наведена на рисунку 1.22.

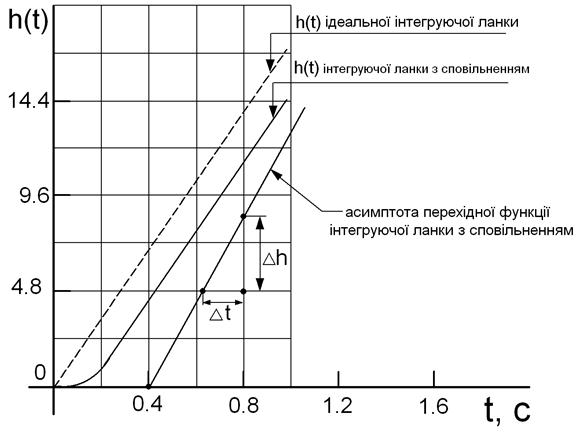
          Рисунок 1.22 ‑ Підсумкова перехідна функція

При  вираз (1.104) перетворюється в вираз

                                                       

і є виразом асимптоти перехідної функції -

По рисунку 1.22  можна вирішити і зворотну задачу, тобто знайти тип і передаткову функцію типової ланки.

Вираз (1.105) дає можливість визначити параметри передаткової функції і тип ланки.

Із рисунка 1.22 параметри мають такі значення:

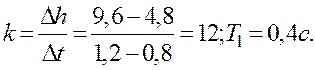
При   - перехідна функція ідеальної інтегруючої ланки з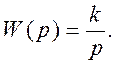

Наявність сталої часу  на рисунку 1.22  вказує на присутність аперіодичної ланки першого порядку з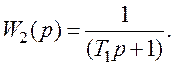

Тоді підсумкова передаткову функція ланки матиме вигляд

                            

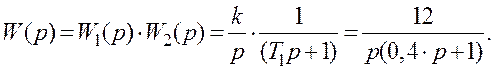
Таким чином, зворотна задача вирішена.

1.6.2 Побудувати часову характеристику h(t) для реальної (з сповільненням) диференційної ланки, якщо k=100 c;

T=0,25 c.

1.6.3 Побудувати часову характеристику h(t) коливальної ланки з передатною функцією 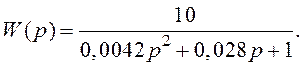 Рекомендується використати [1]-c.64, де наведені відповідні вирази для побудови h(t).

1.6.4 Побудувати часову характеристику h(t) пружної ланки з такою передатною функцією 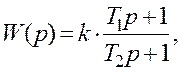 коли  а також для варіанту, коли  Рекомендується використати [3]‑ таблиці А2.

1.6.5 Задані дві динамічні ланки з передатними функціями       

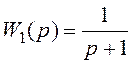 і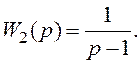

Докажіть, яка з ланок “1” чи “2” має більшу за абсолютною величиною фазу. Доказ проведіть за допомогою частотних характеристик: амплітудно-фазової, та фазочастотної. Як зветься динамічна ланка, що має більшу за величиною фазу.

1.6.6 Розрахуйте та побудуйте амплітудно-фазові характеристики динамічної ланки з передатною функцією 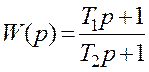 для випадків:

а)

б)

За допомогою АФХ для розглянутих випадків знайдіть максимальний фазовий зсув, що вноситься ланкою в систему. Поясніть, які властивості має ланка при  і  та як її можна використати.

Розв’язання.

Вирази для побудови АФХ і ФЧХ мають вигляд

                       

                                                          

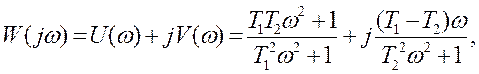
Відповідно для випадків:

                            а)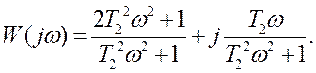                  

При   

          

          

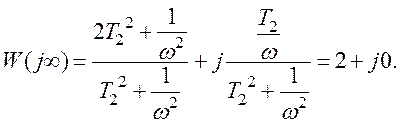
- фазовий зсув позитивний.

                         б)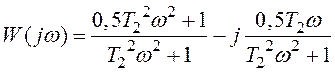                    

При     

            

           

          - фазовий зсув негативний.

Динамічна ланка у випадку а) діє з перевагою властивостей диференційної ланки, а у випадку б) – з перевагою властивостей інтегруючої ланки, тому цю динамічну ланку називають пружною.

Амплітудно-фазова характеристика пружної ланки наведена на рисунку 1.23.

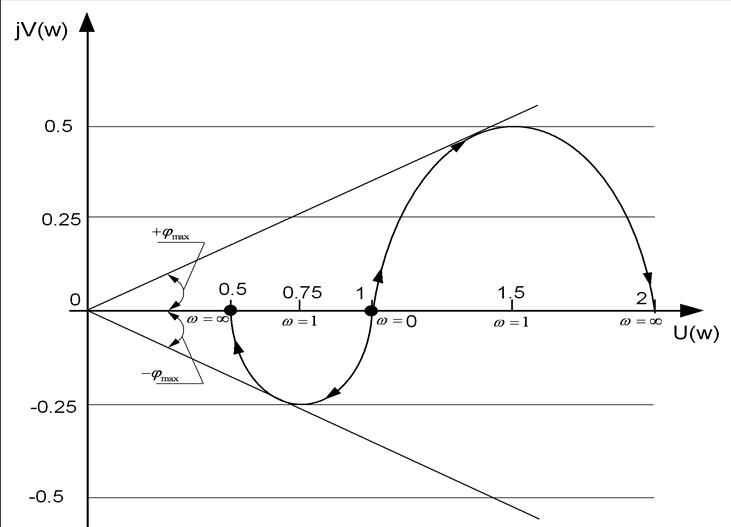
    Рисунок 1.23 ‑ Амплітудно-фазова характеристика пружної ланки

Пружні типові ланки використовують в якості корегуючих ланок при стабілізації нестійких систем, а також з метою підвищення якості систем.

1.6.7 Записати передатну функцію і побудувати ЛАЧХ і ЛФЧХ корегуючої ланки, схема якої наведена на рис. 1.24, без урахування навантаження і з його урахуванням. Зробити висновки щодо впливу опору навантаження.

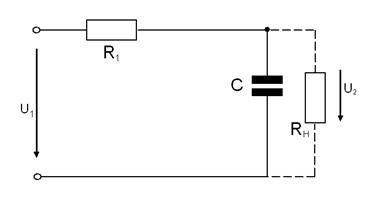
Рисунок 1.6.3 ‑ Принципова схема корегуючої ланки

2. СТІЙКІСТЬ ЛІШІЙНИХ НЕПЕРЕРВНИХ САК

(МОДУЛЬ 2)

2.1 Практичні заняття 7 і 8

Методичні вказівки

Під стійкістю системи автоматичного керування розуміють її властивість повертання в початкове (або близьке до того) положення після закінчення дії факторів (збуджень), які вивели систему із стану початкової рівноваги. Стійкість системи є необхідною умовою можливостей САК вирішувати поставлені перед нею завдання.

Причинами нестійкості системи є:

‑інерційність елементів;

‑великий коефіцієнт підсилення розімкненої системи;

‑структурна нестійкість.

 Задачі, які розв’язують при аналізі стійкості, це:

‑оцінка стійкості САК при заданих параметрах;

‑визначення запасів стійкості;

‑визначення допустимого за умови стійкості діапазону змінення деяких незаданих параметрів систем;

‑з’ясування питання, чи може система при заданій структурі в принципі бути стійкою.

Перші дві задачі вирішуються за допомогою критеріїв стійкості, третя – побудовою зон стійкості; четверта – перевіркою умов структурної стійкості.