Принципи автоматичного керування та математичні моделі лінійних безперервних систем автоматичного керування, страница 6

У цьому разі потрібно вирахувати корні чисельника і знаменника, поліноми розкласти на елементарні множники і далі розв’язувати задачу з виразом (1.77), як задачу з виразом (1.76). Але цей шлях ускладнює процес побудови частотних характеристик.

Для W(p)  у вигляді (1.77) рекомендується наступні вирази для побудови АФХ, АЧХ, ФЧХ і ЛАЧХ:

- для побудови АФХ використовують

    

                                         

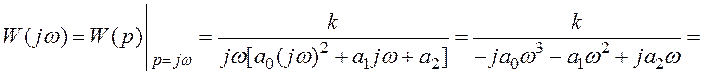
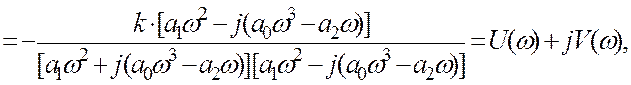
           де      

                                                

                                                   

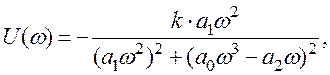
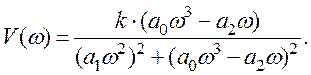
Задаючи ω і ураховуючи за умовами задачі числові значення параметрів  обчислюють по виразам (1.82) та (1.83) відповідні значення, записують їх у таблицю і будують АФХ – W(jω);

- для побудови АЧХ використовують

                                                                       

                                                                 

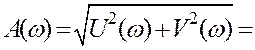
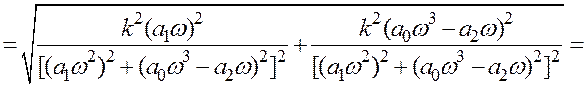
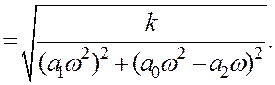
Задаючи ω обчислюють відповідні значення;

- для побудови ФЧХ використовують

               

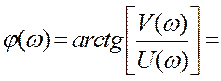
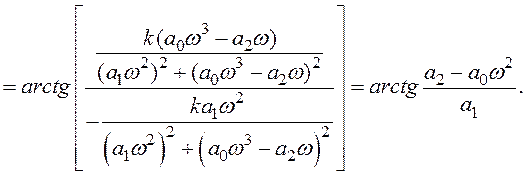
Задаючи ω обчислюють відповідні значення

- для побудови ЛАЧХ використовують рекомендації [11] – c. 88-89.

Відповідно до [11]  визначають відношення коефіцієнтів з більшими індексами до коефіцієнтів з меншими індексами

                                                           

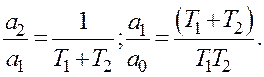
Якщо при записі передатної функції прийняти, що Т₁ > Т₂, то тоді будемо мати такі наближені рівняння

                                                         

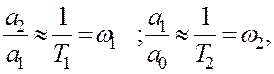
де ω₁, ω_2­­ – частоти сполуки інерційних ланок першого порядку.

Ураховуючи (1.87), при побудові ЛАЧХ для задачі з виразом (1.77) можна використати вираз (1.76), для якого

                    

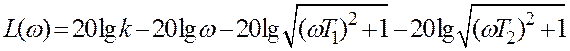
Метод, рекомендований в [11] для побудови ЛАЧХ по коефіцієнтам переданої функції, може бути поширений на загальний випадок, коли передатна функція розімкненої системи має вигляд:

       

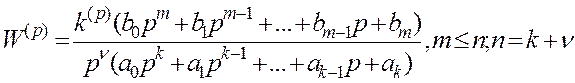
  Із (1.89) визначаються частоти сполуки інерційних ланок:

- чисельника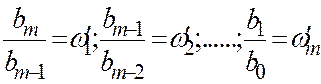                            

- знаменника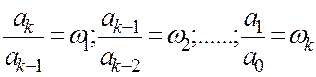                             

Нахил ЛАЧХ на частотах сполуки, які належать знаменнику, дорівнює –, а на частотах сполуки, які належать чисельнику, дорівнює. Низькочастотна асимптота проводиться під нахилом  через точку з координатами,

де   – коефіцієнт підсилення розімкненої системи

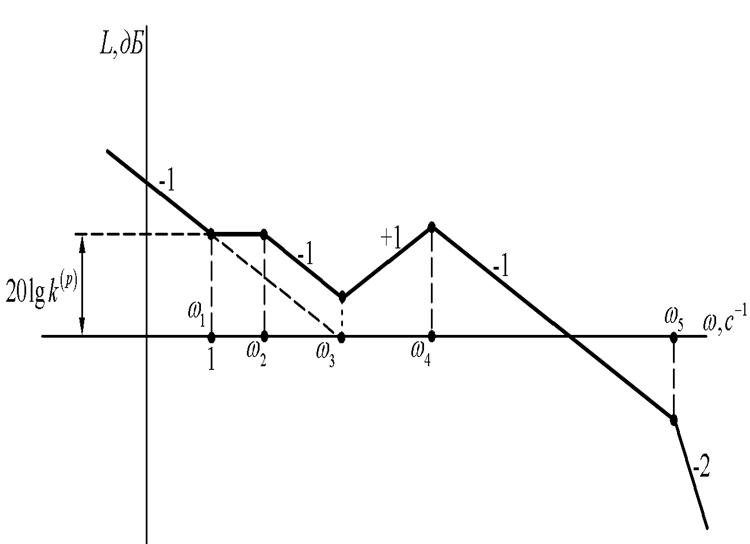
Рисунок 1.20. ЛАЧХ системи 1.5.2

1.5.2 Для двигуна постійного струму з незалежним збудженням, коли вхідною координатою є напруга (U) на затискачах обмотки якоря, а вихідною – швидкість двигуна (ω) побудувати АФХ, АЧХ, ФЧХ і ЛАЧХ  для такого варіанту:. Визначити тип ланки до якої його можна віднести.

1.5.3. Записати передатні функції розімкнених систем автоматичного керування за видом їх ЛАЧХ, що наведенні на рис.1.20. і рис.1.21. 

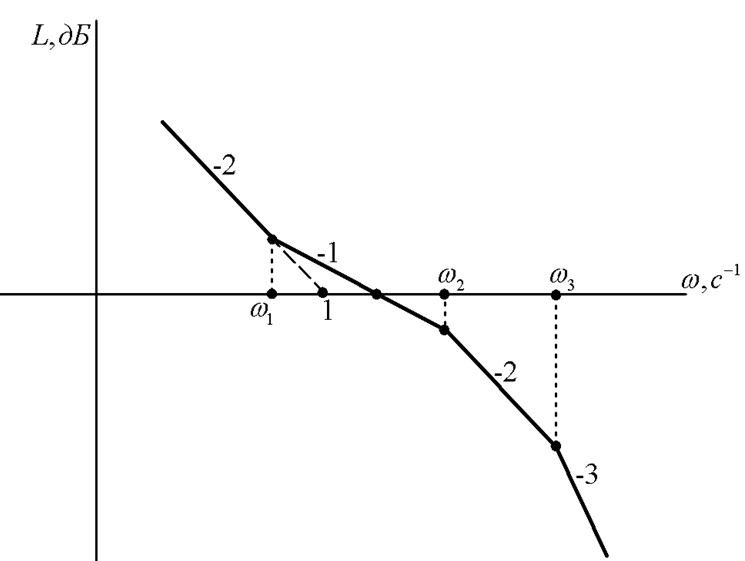
Рисунок 1.21. ‑ ЛАЧХ системи

1.5.4. Побудувати АФХ, АЧХ, ФЧХ, і ЛАЧХ розімкнених систем автоматичного керування з такими передатними функціями:

                                                            

                                                               

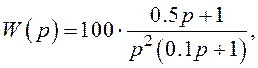
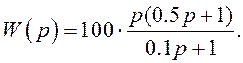
1.5.5. Побудувати ЛАЧХ і ЛФЧХ розімкненої системи, передатна функція  якої має вигляд

                                                   

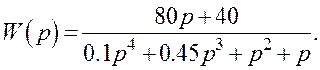
1.6 Практичне заняття 6

Часові і частотні характеристики типових елементів (ланок) САК

Методичні вказівки

Під елементарною ланкою розуміють штучно виділену частину автоматичної системи, яка відповідає будь-якому алгоритму, наприклад, диференціальному рівнянню, порядок якого не більше двох.

Перехідні процеси різних за своїми фізичними принципами дії і конструкціями ланок визначаються подібними диференціальними рівняннями динаміки. З цієї точки зору, до одного типу ланок можна віднести механічну рухому масу і електричне активно-індуктивне коло [1]-с.60.

Якщо одна і та же ланка відповідає різним по своїй природі системам, то така елементарна ланка називається типовою.

Типові ланки – це “цеглини” динамічної споруди, яка називається системою автоматичного керування. Тому дуже важливо знати динамічні властивості та характеристики типових ланок, вміти швидко будувати їх часові і частотні характеристики, визначати ланки, за допомогою яких будуються регулятори (коректуючи пристрої) і за допомогою яких описуються об’єкти керування в автоматизованих електроприводах.

Основними динамічними характеристиками типових ланок є:

–  часова характеристика   x=f(t);

–  перехідна функція   h(t)=x(t), при =1(t);

–  функція ваги (імпульсна перехідна функція) w(t) при = б(t).

Функція ваги є похідною від перехідної функції

                                                                                       

По часовим характеристикам визначають прямі показники якості типової ланки.

Щоб визначити часову характеристику ланки потрібно розв’язати диференціальне рівняння ланки. Розв’язання диференціального рівняння типової ланки не є дуже складною задачею.

Але часові характеристики можна визначити також, використовуючи інші математичні моделі ланок і систем, а саме:

–  передатну функцію ланки – W(p);

–  комплексну передатну функцію ланки і її дійсну частотну характеристику -.

Методика побудови часової характеристики по W(p) викладена в [3]-с.17-24, а по  - в [9] – с.200-206; [11]-114-119.

Для оцінки динамічних і статичних властивостей типових ланок можна скористатись також наближеними методами, серед яких дуже поширеними є частотні.

У загальному випадку диференціальне рівняння типової ланки в операторній формі має вигляд

                                

           де Q(p) і R(p) – поліноми не вище другого порядку.

Поліном Q(p) показує, як швидко та точно реагує типова ланка на вхідну величину. Наявність похідних в Q(p) це спотворення, які вносяться ланкою в систему.

В свою чергу R(p) показує, на що реагує дана ланка і з яким коефіцієнтом передачі (підсилення) вхідна величина з’являється на виході ланки.