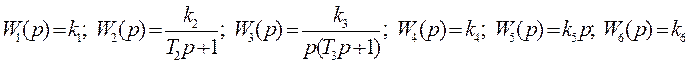
1.4.5. Задана система автоматичного підтримання швидкості двигуна постійного струму, принципова схема якої наведена на рис. 1.19. Скласти структурну схему і записати рівняння системи. Вважати керуючий перетворювач КП інерційною ланкою першого порядку, а двигун Д – ланкою другого порядку. Підсилювач П, тахогенератор ТГ, потенціометр зворотного зв’язку ПЗЗ – пропорційні.
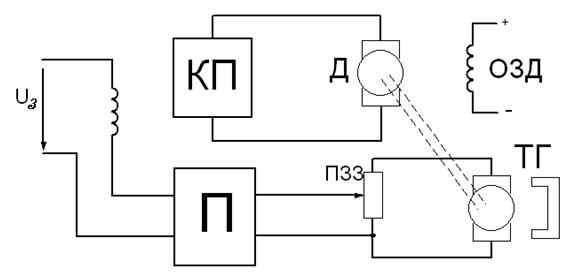
Рисунок 1.19 – Система автоматичного підтримання швидкості
двигуна постійного струму.
1.5 Практичне заняття 5
Математичні моделі динамічних ланок і САК
Частотні характеристики ланок і САК
Методичні вказівки
Частотні характеристики – це формули і графіки, які характеризують реакцію динамічної ланки (системи) на синусоїдну задавальну дію в режимі сталих коливань.
Частотні характеристики, як математична модель динамічних ланок і САК, грають визначну роль для оцінки властивостей САК, їх аналізу та синтезу. За їх допомогою розроблено прості та наглядні методи аналізу і синтезу систем. Тому дуже важливо без помилок і швидко будувати частотні характеристики.
Основною частотною характеристикою є амплітудно-фазова характеристика (АФХ). Вона має ще іншу назву – комплексна передатна функція (КПФ).
У загальному випадку АФХ має вигляд
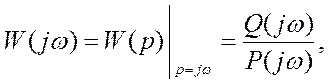
де ![]() – поліноми, або
співмножники.
– поліноми, або
співмножники.
Існує три форми подання АФХ:
- алгебраїчна
![]()
де ![]() – відповідно
дійсна і уявна частотні характеристики (поліноми);
– відповідно
дійсна і уявна частотні характеристики (поліноми);
- показова
![]()
де ![]() – відповідно амплітудно-частотна
і фазочастотна характеристики;
– відповідно амплітудно-частотна
і фазочастотна характеристики;
‑ логарифмічна – це коли частотні характеристики побудовані в логарифмічному масштабі.
У цьому випадку їх називають логарифмічними частотними характеристиками (ЛЧХ).
Перевагами логарифмічних характеристик є більш вдалий масштаб, який дозволяє легко лінеаризувати відповідні характеристики і спростити побудову логарифмічних характеристик групи ланок, а також можливість заміни складніших дій (множення, ділення) простими (додавання, віднімання).
Між формами подання АФХ існує взаємо зв’язок.
У комплексній площині, якщо відомі вирази![]() , можна побудувати
, можна побудувати
![]()
та
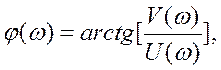
Якщо система складається із типових ланок, а вираз для ![]() має вигляд співмножників у
чисельнику і знаменнику комплексної передатної функції, то
має вигляд співмножників у
чисельнику і знаменнику комплексної передатної функції, то ![]() доцільно знаходити безпосередньо по
доцільно знаходити безпосередньо по ![]() таким чином:
таким чином: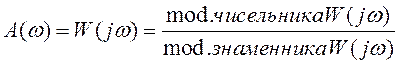 (1.70)
(1.70)
![]()
![]()
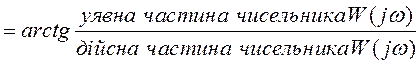
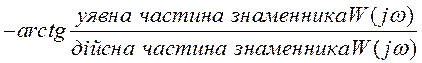
Це вкрай важливо, коли будуються логарифмічні характеристики системи, окремі ланки якої з’єднані послідовно. У цьому разі їх можна одержати, сумуючи амплітудні і фазові логарифмічні характеристики окремих ланок.
Вираз для побудови логарифмічної амплітудно-частотної характеристики (ЛАЧХ) в децибелах має вигляд
![]()
Фазочастотна логарифмічна характеристика![]() будується по виразу (1.69) чи по
виразу (1.71).
будується по виразу (1.69) чи по
виразу (1.71).
При цьому на вертикальній осі відкладають фазу в радіанах
або градусах, а по горизонталі – ω в логарифмічному масштабі. Слід обов’язково пам’ятати,
що побудову асимптотичних ЛЧХ треба починати з характеристик ідеальних
інтегруючих, чи ланок що диференціюють, які мають від’ємний (чи додатний)
нахил 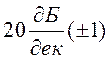 та проходять через точку з координатами
та проходять через точку з координатами
![]() і
і ![]() ,
де
,
де ![]() загальний коефіцієнт підсилення розімкненої
системи.
загальний коефіцієнт підсилення розімкненої
системи.
Наприклад, для 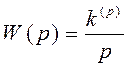 (інтегруюча
ланка)
(інтегруюча
ланка)
![]()
![]()
![]()
При ![]() маємо
маємо
![]()
Порівнюючи (1.73) і (1.74) бачимо, що інтегруюча ланка має
від’ємний нахил на декаду 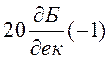
Відзначимо також, що логарифмічна фазочастотна характеристика інтегруючої ланки по (1.71)
![]()
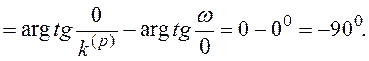
Після побудови інтегруючої чи ланки, що диференціює, знаходять частоти сполуки інерційних, коливальних, форсуючих і інших ланок, при яких змінюються нахили логарифмічних амплітудно-частотних характеристик і будуть ЛАЧХ системи.
Для вирішення задач цього підрозділу рекомендується використати матеріал: [1] – c. 72-94; [2] – c. 64-69; [3] – c. 24-26, 44-51; [4] – c. 37-69; [9] – c. 57-58,72-107; [10] – c. 19-24; [11] – c. 67-89, а також конспект лекцій.
1.5.1 Записати вирази для побудови АФХ, АЧХ, ЛАЧХ і ФЧХ для ланки системи, передатна функція якої
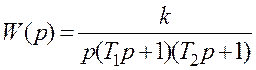
або
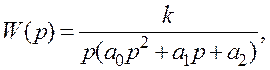
де ![]()
Розв’язання.
У виразі (1.76) передатна функція ланки системи зображена у вигляді включених послідовно двох аперіодичних ланок першого порядку і однієї інтегруючої, тобто у вигляді добутку співмножників.
У цьому разі краще використати для побудови АФХ, АЧХ, ЛАЧХ і ФЧХ формули (1.70) і (1.75).
Вираз для побудови амплітудно-частотної характеристики ![]() матиме вигляд
матиме вигляд
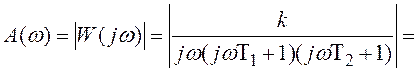
![]()
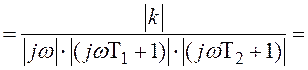
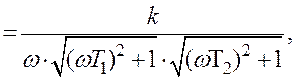
![]()
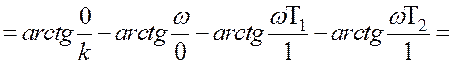
![]()
Змінюючи частоту гармонічного сигналу від 0 до ![]() по виразам (1.78) і (1.79) будуємо
АЧХ і ФЧХ ланки.
по виразам (1.78) і (1.79) будуємо
АЧХ і ФЧХ ланки.
Ці вирази можна використати також для графоаналітичної
побудови АФХ, тобто її годографа по точкам с координатами ![]() і
і![]() ,
,
де ![]() .
.
Для побудови ЛАЧХ вираз (1.78) є дуже зручним для логарифмування.
Вираз для
![]() у відповідності з (1.78)
матиме вигляд
у відповідності з (1.78)
матиме вигляд
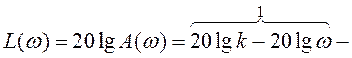
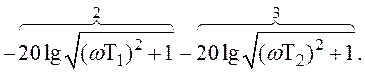
Він складається із трьох асимптот 1, 2 і 3 та двох частот
сполуки 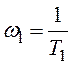 та
та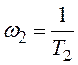 .
.
Шлях запису виразів для побудови АФХ, АЧХ, ФЧХ і ЛАЧХ при розв’язанні задачі з W(p) у вигляді (1.77) буде декілька іншим, тому що передатна функція ланки (часто розімкненої складної системи) не є дріб, у якої чисельник і знаменник зображені як здобуток передатних функцій елементарних ланок, а є дріб, у якої чисельник і знаменник зображені як відношення поліномів.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.