Принципи автоматичного керування та математичні моделі лінійних безперервних систем автоматичного керування, страница 3

Для дослідження систем автоматичного керування, в залежності від умови задачі, використовують для вихідної координати такі передатні

функції:

за завданням

                                                            

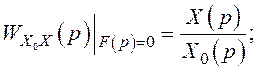
за збуренням

                                                              

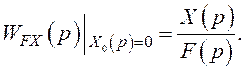
Чи відповідні передатні функції для похибки:

                                                          

                                                          

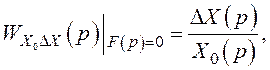
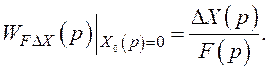
Після цього записують вираз для вихідної координати

                                 

аналогічно для похибки

                            

Вирази (1.27) і (1.28) – це диференціальні рівняння замкненої системи в операторній формі.

Для аналізу і синтезу замкнених систем автоматичного керування широко використовують також передатну функцію розімкненої системи

                                                        

де  – передатна функція прямого ланцюга системи;

      – передатна функція зворотного ланцюга системи.

Тут і подальше:

 – вхідна величина (жадане діяння), – вихідна величина,

– збурення, – похибка.

Для вирішення задач цього підрозділу рекомендується використати матеріал: [1] – c. 71-80; [2] – c. 58-64; 75-86; [5] – c. 203-209; [9] – c. 49-53; а також конспект лекцій.

1.3.1 Записати передатну функцію для схеми, наведеної на рисун-

ку 1.6, використовуючи вираз (1.21)

Розв’язання:

Записуємо диференціальне рівняння (1.21) в операторній формі при нульових початкових умовах

        

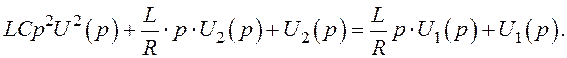
Чи 

                                

З (1.31) одержуємо передатну функцію

                                                 

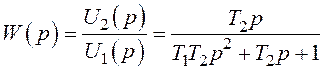
Передатна функція записана в стандартній формі і складається з двох типових ланок:

-  форсуючої з 

                                                                             

-  ланки другого порядку з

                                            ;                  

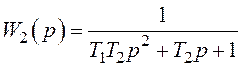1.3.2 Одержати передатну функцію і скласти диференціальне рівняння ланки, схема якої наведена на рис.1.8

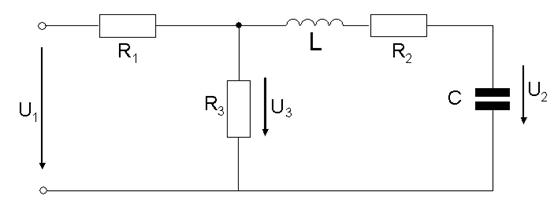
                        Рисунок 1.8 - Принципова схема електричної ланки

Розв’язання.

Передатна функція електричної ланки

                       

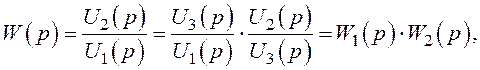
     де

                   

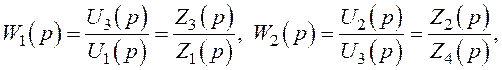
 – операторні опори.

У відповідності з рис.1.8 операторні опори мають такі вирази:

             

                                           

                                                                                      

                                                                  

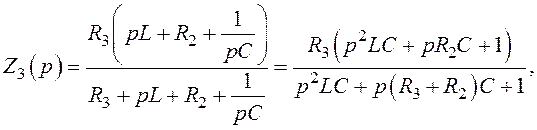
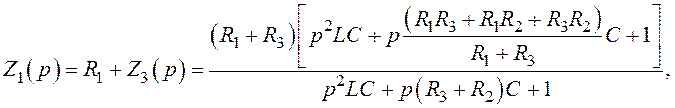
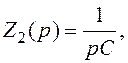
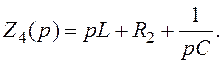
Тоді, ураховуючи вирази (1.37)÷(1.40), маємо

     

                                                              

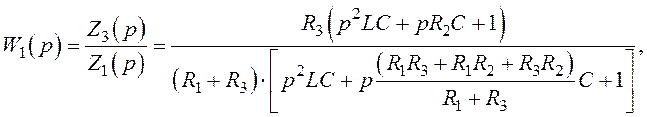
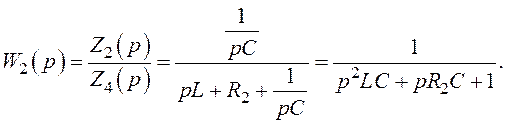
Отже

                                                                         

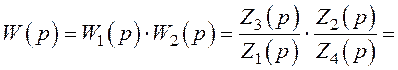
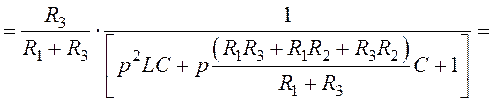
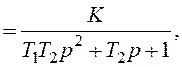
де  .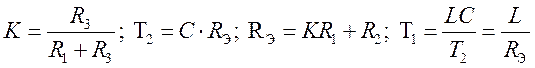

По передатній функції записуємо диференціальне рівняння в зображеннях по Лапласу наступним чином

                                                                  

        Чи

                                             

Формальна заміна символу p на символ   дає запис диференціального рівняння в оригіналах

                                 

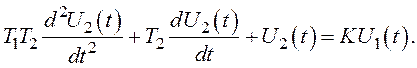
1.3.3 Одержати передатну функцію і скласти диференціальне рівняння ланки, схема якої наведена на рис.1.8, за умови, що напруга на котушці індуктивності , а не на конденсаторі С.

1.3.4 Записати передатні функції та скласти по ним структурні схеми електродвигуна постійного струму незалежного збудження, використовуючи рівняння (1.5÷1.8) – форма ВВ, а також рівняння (1.15) – форма ЗС .

Визначити, якими типовими ланками він постає на структурних схемах.

Розв’язання.

В зображеннях по Лапласу рівняння (1.5) та (1.6) мають такий вигляд:

                                                    

чи   

                                                     

                          

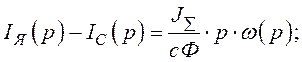
чи

                                        

     де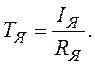 

Використовуючи рівняння (1.48) і (1.50), будуємо структурну схему. Але раніше знаходимо передатні функції електродвигуна, з яких буде складатися структурна схема.

                               –             

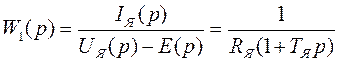аперіодична ланка першого порядку;

        

     де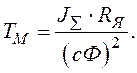                                                                                      

          W₂(p) – інтегруюча ідеальна ланка.

           – без інерційна ланка.                             (1.53)

Таким чином, на структурній схемі електродвигун постає трьома ланками: аперіодичною першого порядку, ідеальною інтегруючою і без інерційною. Структурна схема наведена на рис.1.9

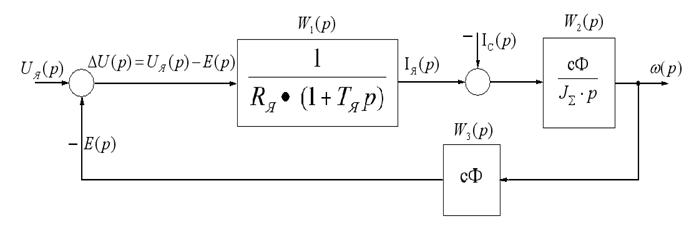
            Рисунок 1.9 - Структурна схема електродвигуна постійного

струму незалежного збудження (форма ВВ)

В зображеннях по Лапласу система рівнянь (1.15) має вигляд:

                   

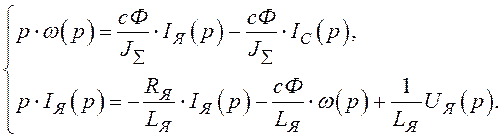
      Цій системі відповідає структурна схема, яка наведена на рисунку 1.10

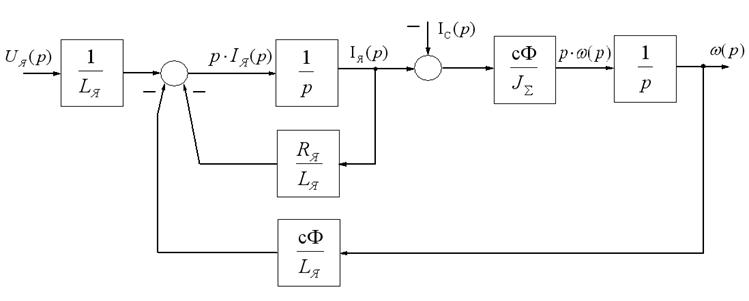
Рисунок 1.10 - Структурна схема електродвигуна постійного

струму незалежного збудження (форма ВВ)

1.3.5 Записати передатні функції та скласти по ним структурну схему електродвигуна постійного струму незалежного збудження при керуванні напругою якоря, коли ; ; (дивись задачу 1.2.2.) .

Визначити, якими типовими ланками він постає на структурній схемі. Де   – кут повороту вала.

1.3.6 Записати передатні функції та скласти по ним структурну схему електродвигуна постійного струму незалежного збудження при керуванні напругою якоря, коли (дивись задачу 1.2.3). Де М – обертальний момент двигуна.

Визначити, якими типовими ланками він постає на структурній схемі.

1.3.7 Операційний підсилювач охоплено від’ємними зворотнім зв’язком ЗЗ. Записати передатну функцію, скласти диференціальне рівняння, а також визначити тип регулятора. Схеми підсилювачів наведені на рисунку 1.11 і рисунку 1.12

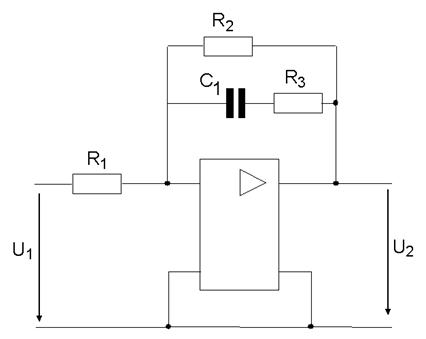
                                 Рисунок 1.11 - Принципова схема підсилювача

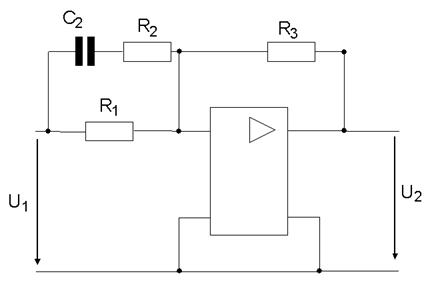
                                Рисунок 1.12 - Принципова схема підсилювача