Дослідження якості САК виконується на основі розв’язання рівнянь замкненої системи, а також за допомогою наближених методів оцінки якості.
Треба пам’ятати, що якість лінійних САР залежить не тільки від вигляду коренів характеристичного рівняння, а й від початкових умов. Стійкість же лінійних САР залежить лише від коренів характеристичного рівняння.
Якість усталених режимів (статичного і динамічних ) оцінюють за допомогою наступних методів:
‑по теоремі операційного числення про кінцеве значення оригіналу;
‑по методу коефіцієнтів помилок.
Останній метод дістав значене поширення для знаходження помилок особливо в слідкуючих і програмних САК.
Якість перехідних процесів зручно оцінювати за допомогою частотних характеристик:
‑дійсної частотної характеристики замкненої системи (ДЧХ);
‑амплітудно-частотної характеристики замкненої системи (АЧХ);
‑логарифмічних амплітудно і фазочастотних характеристик розімкненої системи (ЛАЧХ і ЛФЧХ).
Треба також пам’ятати, що частотні характеристики пов’язані
з перехідною функцією мінімально-фазових систем і є наближеними методами оцінки
якості перехідних процесів. Частотні характеристики визначають показники якості
перехідного процесу по частоті позитивності ![]() показнику
коливальності М АЧХ, частоті зрізу
показнику
коливальності М АЧХ, частоті зрізу ![]() та
та ![]() (коли фаза має значення
(коли фаза має значення![]() ) ЛАЧХ.
) ЛАЧХ.
Якщо треба дати точну оцінку якості перехідного процесу, то використовують аналітичні методи розв’язання диференціальних рівнянь, або проводять структурне модулювання системи на цифровій обчислювальній машині.
При вирішенні задач цього розділу і підготовці до практичного заняття бажано повторити матеріал за літературою: [1]-c. 193-227; [2]-c. 146-158, c. 195-213; [4]-c. 162-187; [9]-c. 181-208; [11]-c.107-129.
3.1.1
Визначити сумарну похибку слідкуючої системи, структурна схема якої наведена на
рис. 3.1, коли на неї діє вхідний сигнал 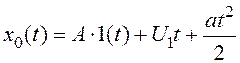 і
збурення
і
збурення ![]() де
де ![]() -
константи.
-
константи.
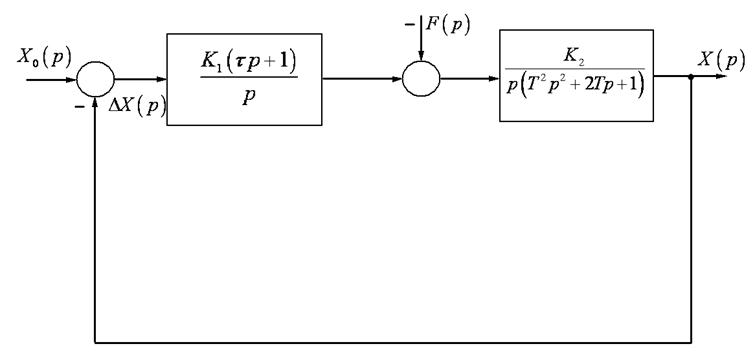
Рисунок 3.1 ‑ Структурна схема слідкуючої системи
Розв’язання
З методологічної точки зору розглянемо вирішення цієї задачі як по теоремі операційного числення про кінцеве значення оригіналу, так і по методу коефіцієнтів помилок.
Згідно з теоремою
![]()
![]()
![]() (3.1)
(3.1)
По структурній схемі, наведеній на рисунку 3.1, визначаємо
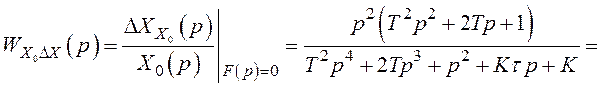
![]() (3.2)
(3.2)
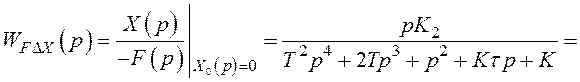
![]() (3.3)
(3.3)
Із виразів (3.2) і (3.3) одержуємо
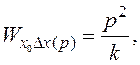 (3.4)
(3.4)
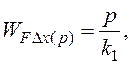 (3.5)
(3.5)
де
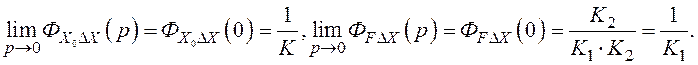
Підставляємо (3.4) і (3.5) в формулу (3.1), тоді маємо
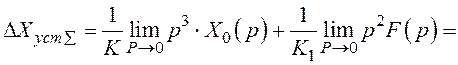
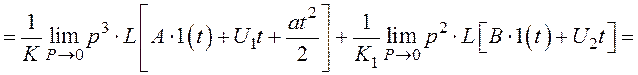
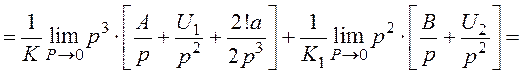
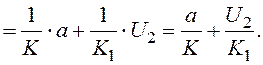 (3.6)
(3.6)
Аналізуючи вираз (3.6), робимо такі висновки:
1. помилка прямо пропорційна величині зовнішньої дії;
2. помилка по каналу ![]() обернено
пропорційна коефіцієнту підсилення
обернено
пропорційна коефіцієнту підсилення ![]() розімкненої
системи (
розімкненої
системи (![]() );
);
3. помилка по каналу ![]() обернено
пропорційна коефіцієнту підсилення тих ланок системи, які розташовані між координатами
обернено
пропорційна коефіцієнту підсилення тих ланок системи, які розташовані між координатами
![]() та F (в нашому випадку це
коефіцієнт
та F (в нашому випадку це
коефіцієнт![]() ).
).
Цю задачу можна вирішити інакше (значно простіше), якщо виконати такі дії:
‑визначити порядок астатизму системи по каналам передачі
інформації ![]() та
та![]() ,
використовуючи структурну схему. По кількості інтегруючих ланок між виходом
системи (помилкою) і зовнішньою дією (задавальною або збурювальною), які
структурно попадають в негативний зворотний зв'язок, маємо
,
використовуючи структурну схему. По кількості інтегруючих ланок між виходом
системи (помилкою) і зовнішньою дією (задавальною або збурювальною), які
структурно попадають в негативний зворотний зв'язок, маємо ![]() а
а![]() .
.
‑ указати, які із помилок по завданню та по збуренню будуть дорівнювати нулю згідно з визначеним порядком астатизму;
‑ урахувати висновки, які були зроблені при аналізі виразу (3.6).
Так, наприклад, по каналу ![]() між
між
![]() і
і ![]() структурно
розташовуються дві інтегруючі ланки, отже
структурно
розташовуються дві інтегруючі ланки, отже ![]()
При ![]() статична і
динамічна по швидкості помилки відсутні, тобто дорівнюють нулю.
статична і
динамічна по швидкості помилки відсутні, тобто дорівнюють нулю.
Будемо чекати тільки помилку динамічну по прискоренню, яка
згідно з висновками стосовно виразу (3.6), дорівнює 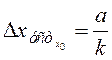 (перша
частина виразу 3.6). Задача вирішена.
(перша
частина виразу 3.6). Задача вирішена.
Далі розв’язуємо задачу по методу коефіцієнтів помилок.
Згідно з цим методом
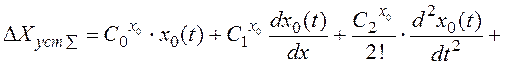
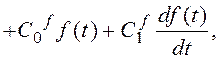 (3.7)
(3.7)
де ![]()
![]()
![]()
![]()
![]() -
відповідно коефіцієнти помилок по завданню
-
відповідно коефіцієнти помилок по завданню ![]() та
по збуренню
та
по збуренню ![]()
Кількість коефіцієнтів визначається змістом виразів для ![]() і
і ![]() за
умовами задачі.
за
умовами задачі.
У виразі для ![]() присутні всі три
типові усталені рухи (нерухомий стан, рух із сталою швидкістю, рух із сталим
прискоренням). У виразі для
присутні всі три
типові усталені рухи (нерухомий стан, рух із сталою швидкістю, рух із сталим
прискоренням). У виразі для ![]() є тільки
нерухомий стан та рух із сталою швидкістю. Цим типовим усталеним рухам
відповідають коефіцієнти помилок з індексами “0”, “1”, “2”.
є тільки
нерухомий стан та рух із сталою швидкістю. Цим типовим усталеним рухам
відповідають коефіцієнти помилок з індексами “0”, “1”, “2”.
Існує два способи визначення коефіцієнтів помилок. Обидва способи базуються на передатних функціях відносно помилок по завданню (3.2) та по збуренню (3.3)
Щоб визначити коефіцієнти помилок по першому способу розділимо многочлен чисельника на многочлен знаменника відповідно у виразах (3.2) і (3.3).
Після ділення будемо мати:
‑
По каналу ![]()
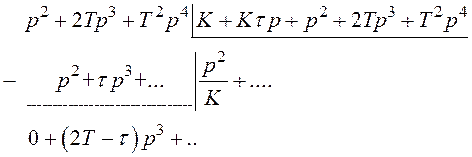
Далі ділити нема сенсу, тому що вже з’явився останній
коефіцієнт 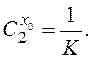 Коефіцієнти
Коефіцієнти ![]() і
і
![]() дорівнюють нулю. Вони відсутні у
виразі, що є результатом ділення.
дорівнюють нулю. Вони відсутні у
виразі, що є результатом ділення.
‑
по каналу ![]()
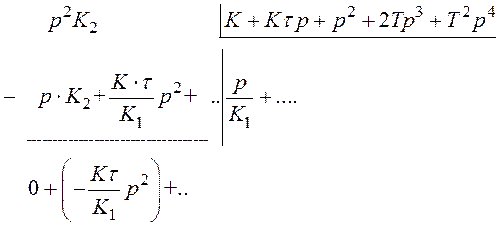
Далі ділити нема
сенсу, тому що вже з’явився останній коефіцієнт 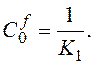
Коефіцієнт ![]()
Треба також пам’ятати, що коефіцієнти статичної помилки ![]() швидкісної помилки
швидкісної помилки ![]() і помилки за прискоренням
і помилки за прискоренням ![]() зв’язані з порядком астатизму системи
таким чином:
зв’язані з порядком астатизму системи
таким чином:
‑
при![]() :
: ![]()
![]()
![]() (у
нашому випадку
(у
нашому випадку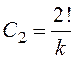 );
);
‑
при ![]()
![]() ;
; ![]() (
(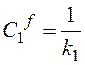 ).
).
Відповідно з (3.7) після визначення коефіцієнтів помилок обчислюємо
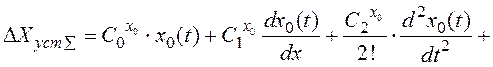
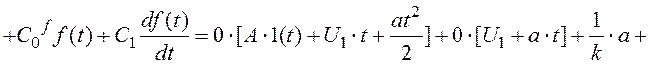
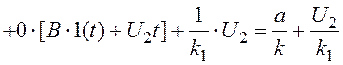 (3.8)
(3.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.