Прийняти наступні допущення:
1) реакція якоря, вихрові струми, гістерезіс – нехтовно малі;
2) індуктивність ОЗ (обмотки збудження) – величина стала.
Принципова схема електродвигуна наведена на рисунку 1.5
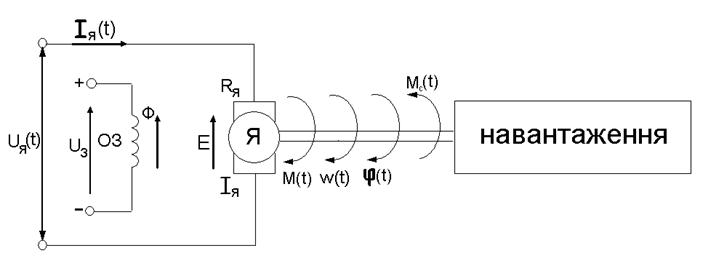
Рисунок 1.5 - Принципова схема електродвигуна постійного
струму незалежного збудження.
Розв’язання
При зроблених допущеннях динамічні процеси в електродвигуні описуються наступними рівняннями:
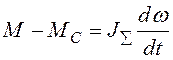
рівняння руху електропривода
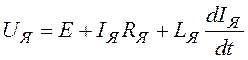
рівняння електричної рівноваги в якірному ланцюгу електродвигуна
Доповнюємо (1.5) і (1.6) рівняннями:
![]()
![]()
В рівняннях (1.5÷1.8) прийняті такі літерні позначення параметрів електродвигуна:
J∑ – сумарний момент інерції;
Rя – активний опір обмотки якоря;
Lя – індуктивність обмотки якоря;
Ф – потік обмотки збудження.
При Ф=const M≡Iя; Mс≡Ic і E≡ω.
З виразу (1.5) визначаємо
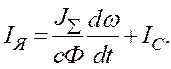
Диференціюємо (1.9) при Ic= const (за умовами задачі).
Тоді
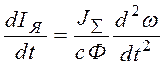
Підставляємо (1.9) і (1.10) в вираз (1.6) і отримуємо
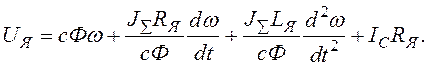
Ураховуючи умовності запису диференціальних рівнянь (дивись методичні вказівки), переписуємо вираз (1.11) в стандартній формі ВВ.
![]()
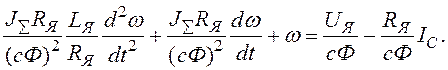
Чи
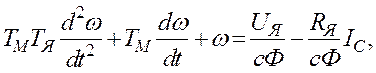
де 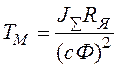 –
електромеханічна стала часу,
–
електромеханічна стала часу,
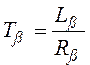 –
електромагнітна стала часу.
–
електромагнітна стала часу.
Розмірність [TM] = 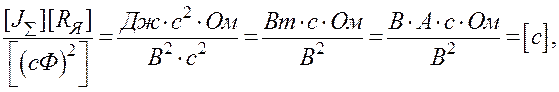
[TM] =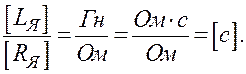
Рівняння [1.13] в сталому режимі має вигляд
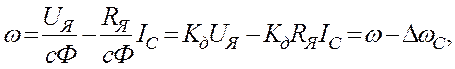
де Kд – коефіцієнт передачі електродвигуна.
Рівняння (1.14) – це електромеханічна характеристика.
Форма ЗС (форма змінних стану) є природною формою запису диференціального рівняння для електродвигуна постійного струму з незалежним збудженням. Для цього потрібно вирази (1.5) і (1.6) вирішити відносно похідних струму і швидкості.
Маємо
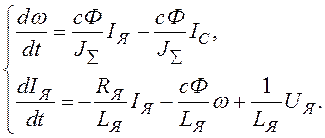
В матричній формі система (1.15) має вигляд
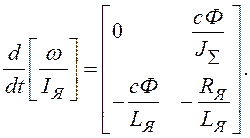
В інших випадках перехід від форми ВВ до форми ЗС виконується по методиці, викладеній в [1] – c. 80-83
1.2.2 Скласти диференціальне рівняння двигуна постійного струму незалежного збудження при керуванні напругою якоря, коли x0=UЯ(t); x(t)=φ; UЗ=const.
1.2.3 Скласти диференціальне рівняння двигуна постійного струму незалежного збудження при керуванні напругою якоря, коли x0=UЯ(t); x(t)=M(t); UЗ=const.
1.2.4 Скласти диференціальне рівняння ланки, принципова схема якої наведена на рисунку 1.6
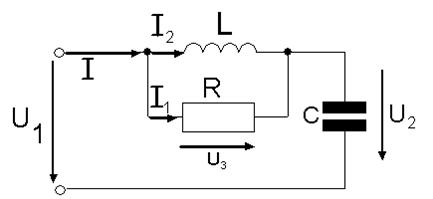
Рисунок 1.6 -‑ Принципова схема ланки електричного
ланцюга
Розв’язання
Використовуючи закони Ома і Кіргофа, записуємо наступні вирази
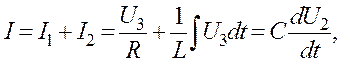
![]()
Підставляємо формулу (1.18) в (1.17).
Тоді маємо
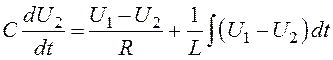
Диференціюємо вираз (1.19) і записуємо його в стандартній формі
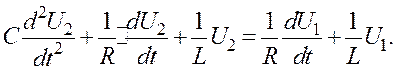
Помножуємо ліву і праву частину виразу (1.20) на L, тоді маємо
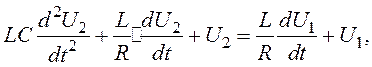
де
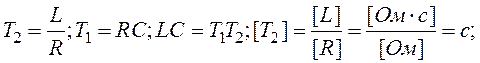
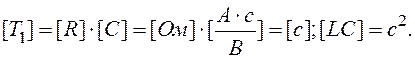
1.2.5 Дві однакові ланки з резистором і конденсатором включені послідовно. Записати диференціальне рівняння. Принципова схема наведена на рисунку 1.7
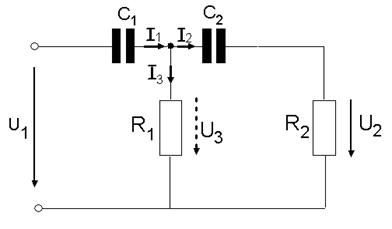
Рисунок 1.7 - Принципова схема пасивної ланки
Рекомендації до розв’язання: використати метод контурних струмів, чи принцип накладання (суперпозиції).
1.2.6 Дві одинакові ланки з резистором і конденсатором включені послідовно. Записати диференціальне рівняння для того випадку, коли можна знехтувати впливом наступної ланки (з R2 – C2) на попередню
(з R1 – C1). Принципова схема наведена на рис.1.7.
Рекомендації до розв’язання: Прийняти I2=0. Зв’язати U3 з U1, потім U2 з U3 і вилучивши U3, записати диференціальне рівняння відносно координат U1 і U2.
1.3 Практичне заняття 3
Математичні моделі динамічних ланок і САК .
Передатні функції.
Методичні вказівки
Визначення передатної функції виходить з відомого перетворення Лапласа, згідно з яким деяка функція часу f(t) – оригінал – може бути перетворена в функцію комплексної величини p=σ+jω відповідно формулі прямого перетворення
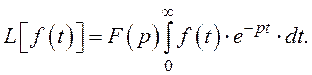
Передатну функцію W(p) представляють як відношення зображень по Лапласу вихідної і вхідної величини при нульових початкових умовах.
Передатну функцію записують так:
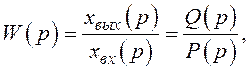
де Q(p),P(p) – відповідні оператори.
Відзначимо що передатна функція, як математична модель динамічних ланок і САК, надзвичайно поширена і використовується з метою:
- відображення динамічних властивостей елементів (систем) на
основі структурних алгоритмічних схем;
- побудови диференціального рівняння (якщо потрібно) шляхом
формальної заміни символу p=σ+jω на символ ![]() ;
;
- знаходження комплексної передатної функції (амплітудно-фазової
характеристики) і на її основі виразів для побудови частотних
характеристик, на яких базуються різні методи дослідження
елементів і систем;
- застосування математичного апарату, зручного для спрощення
структурних схем, а також для структурного моделювання.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.