Принципи автоматичного керування та математичні моделі лінійних безперервних систем автоматичного керування, страница 8

При дослідженні замкнутих систем за допомогою критеріїв Рауса, Гурвіца, Михайлова необхідно обов’язково визначити спочатку передатну функцію замкненої системи, якщо відома передатна функція розімкненої.

. Також треба пам’ятати, що у всіх випадках, коли задається передатна функція чи частотна характеристика розімкненої системи, мається на увазі, що вона замикається одиничним від’ємним зворотним зв’язком. Треба також знати, що необхідною умовою стійкості системи є позитивність всіх коефіцієнтів її характеристичного рівняння.

Треба також пам’ятати, що частотний критерій Михайлова для аналізу стійкості замкнених систем використовує характеристичний поліном замкненої системи, але частотний критерій Найквіста використовує відповідні частотні характеристики (АФХ, ЛАЧХ, ЛФЧХ) розімкнених систем, за допомогою яких визначають стійкість замкнених.

Для визначення запасів стійкості по модулю (амплітуді) і по фазі використовуйте критерій Найквіста, розроблений для частотних характеристик розімкнених систем.

Критичне значення коефіцієнта підсилення розімкненої системи (або іншого параметра) можна визначити по любому критерію стійкості (алгебраїчному або частотному).

Дослідження стійкості, тобто виявлення впливу окремих параметрів (або параметра) на стійкість системи при фіксованих значеннях інших параметрів, вирішується за допомогою вище названих критеріїв стійкості, але зі зростанням порядку системи рівнянь розрахунки різко ускладнюються. Тому при високих порядках системи () рекомендується для дослідження стійкості використати метод D – розбиття.

Якщо у системі автоматичного керування є ланка з запізненням, то незалежно от місця її знаходження в системі характеристичне рівнянням замкненої системи матиме вигляд

                                                                                  

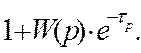
Це рівняння є трансцендентним і має нескінченну кількість коренів, які для стійкої системи повині розміщуватись у лівій площині коренів. Знаходження коренів у цьому випадку – трудомістке завдання, тому для аналізу стійкості таких систем найбільш прийнятним є використання частотного критерію Найквіста.

Зовнішньою ознакою структурно – нестійкої системи є відсутність

 ( рівність нулю) в лінійному характеристичному рівнянні замкненої системи деяких членів (коефіцієнтів), або присутність в системі двох і більше інтегруючих ланок  при інших аперіодичних ланках. У таких систем для досягнення стійкості необхідна зміна структурної схеми.

При вирішенні задач цього розділу бажано повторити матеріал за літературою: [1] – c.140-191; [2] – c.159-194; [4] – c.84-113; [9] – c.143-180; [11] – c.89-107.

2.1.1 Передатна функція розімкненої системи має вигляд

                                                  

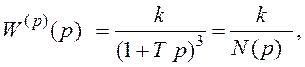
              де k=10; T=1c.

Визначити стійкість замкненої системи, а також критичне значення коефіцієнта підсилення розімкненої системи, використовуючи критерії Гурвіца, Рауса, Михайлова і Найквіста.

Розв’язання.

Згідно з методичними вказівками структурна схема замкненої системи буде такою

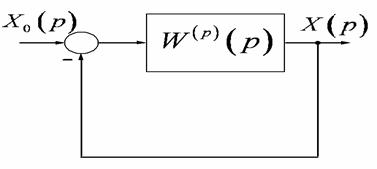
Рисунок 2.1‑ Структурна схема замкненої системи

Відповідно до рисунку2.1 записуємо передатну функцію замкненої

системи

                              

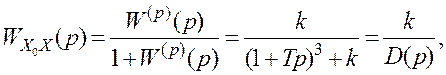
     де для одиночного зворотного зв’язку

                                                                                 

В подальшому вираз (2.4) використовуємо для визначення стійкості замкненої системи.

а)   Критерій Гурвіца

       Визначаємо D(p)

                                                              

                де    

Необхідна умова стійкості виконується тому, що всі коефіцієнти виразу (2.5) – позитивні.

Перевіряємо виконання достатньої умови стійкості. Для цього складаємо головний визначник і діагональні мінори Гурвіца

                        

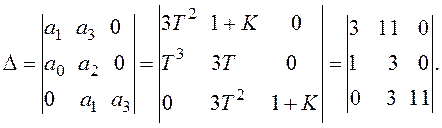
Із головного визначника Гурвіца виписуємо діагональні мінори

  

                                                                 

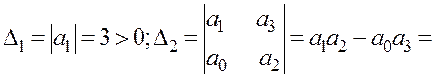
Вираз (2.7) вказує на те, що система нестійка. Для системи 3-го порядку умовою стійкості є   (звичайно, при   ).

Щоб визначити критичне значення коефіцієнта підсилення потрібно в головний визначник Гурвіца замість  підставити  і відносно  розкривати мінор

В цьому розі мінор  має вигляд

                             

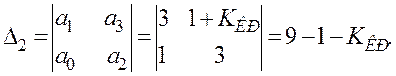
Із виразу (2.8) визначаємо = 8.

Аналізуючи умови стійкості, бачимо, що в теоретичному плані стійкість даної системи може бути досягнута за рахунок:

‑зменшення передаткового коефіцієнта розімкненої системи шляхом зменшення будь-якого коефіцієнта передачі, які як співмножники входять до складу k;

‑розсування сталих часу.

Розглянемо останній випадок докладніше за умови, що

                                                  

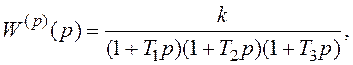
          де   

В цьому випадку

                

Визначаємо

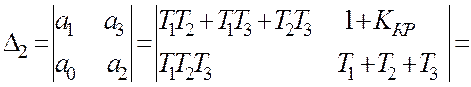
Чи   або  .

При виборі варіанта настроювання системи насамперед слід виходити з ефективності і технічної зручності вибору зміни регулюючого параметра системи.

Часто стійкість даної системи досягається за рахунок одночасної зміни в потрібному напрямку сталих часу і коефіцієнтів передачі.

Слід пам’ятати, що критичне значення коефіцієнта передачі залежить не від абсолютного значення сталих часу, а від їх співвідношення.

б) Критерій Рауса

 Раус запропонував критерій у вигляді алгоритму, на основі якого складається таблиця для оцінки стійкості системи. Критерій Рауса легко програмується і дозволяє у випадку нестійкості системи визначити число правих полюсів.

Таблиця Рауса складається згідно з виразом (2.5) і має такий вигляд

           Таблиця 2.1 ‑ Таблиця Рауса