МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра АУТПТЭК
на тему :«Синтез системы регулирования с использованием
последовательной коррекции»
по курсу: «Теория автоматического управления»
Выполнил: ст. гр. АКТ-02-2
Абрамов А.В.
Приняла: асс. каф.
Марусей О. В.
Алчевск, 2005
ЗАДАНИЕ
Провести синтез последовательного корректирующего устройства заданной системы, структурная схема которой приведена на рисунке 1.
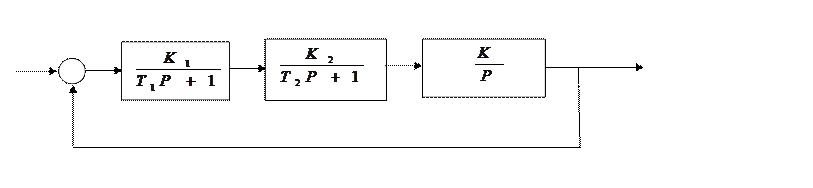
Рисунок 1 – Структурная схема заданной системы
Исходные данные:
K =0.1 ; T1 =0.01 ;
K1 = 10; T2 = 0.07.
K2 = 20;
СОДЕРЖАНИЕ
Введение 4
1. Анализ нескорректированной АСР 5
1.1 Передаточная и комплексно – частотная функции системы 5
1.2 Расчет переходного процесса САУ 6
1.3 Расчет точности системы 7
2. Анализ устойчивости исследуемой АСР 8
2.1 Критерий Гурвица 8
2.2 Исследование устойчивости критерием Михайлова 9
3. Построение частотных характеристик 10
4. Синтез корректирующего устройства 16
Заключение 20
Перечень ссылок 21
ВВЕДЕНИЕ
Синтезом системы автоматического регулирования называется выбор структурной схемы и значений параметров ее отдельных звеньев, обеспечивающих заданную точность в установившемся режиме и характер переходного процесса, удовлетворяющий заданным показателям качества.
При синтезе систем автоматического регулирования всегда имеются серьезные ограничения в выборе структуры системы и параметров отдельных звеньев. Заданными, не подлежащими к изменению, обычно являются характеристики регулируемого объекта. Полностью или частично ограничен выбор элементов, входящих в систему (исполнительных элементов, усилителей, датчиков и др.). Система автоматического регулирования может быть разбита на неизменяемую часть и изменяемую части, причем изменяемой частью оказываются корректирующего устройства.
Корректирующим называются устройства с легко изменяемыми параметрами и характеристиками, вводимые в состав систем автоматического регулирования для придания им требуемых динамических свойств – обеспечения устойчивости систем автоматического регулирования и улучшения показателей качества переходного процесса.
Корректирующие устройства по способу включения в систему автоматического регулирования делятся на параллельные и последовательные. В данном курсовом проекте используется последовательное корректирующее устройство.
Практически синтез систем автоматического регулирования сводится к выбору общего коэффициента усиления системы для обеспечения заданной точности в установившемся режиме и к синтезу корректирующих устройств для обеспечения заданных показателей качества переходного процесса.
1. АНАЛИЗ НЕСКОРРЕКТИРОВАННОЙ АСР
1.1 Передаточная и комплексно – частотная функции системы
Можно получить эквивалентную передаточную функцию замкнутой АСР в общем виде:
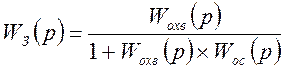 ,
(1.1)
,
(1.1)
Так как звенья соединяются последовательно, то при нахождении эквивалентной передаточной функции они перемножаются:
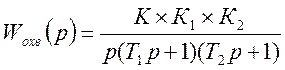
Если подставить заданные значения, то получится передаточная функция вида:
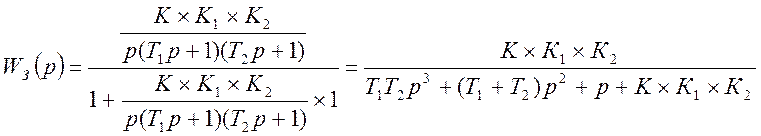 ;
;
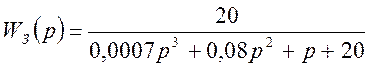 . (1.2)
. (1.2)
Комплексно – частотная функция замкнутой системы может быть получена путем замены оператора Лапласа на оператор Фурье в выражении 1.2:
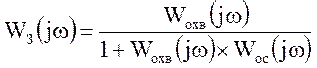 ;
;
И с подстановкой значений комплексно–частотная функция замкнутой системы будет иметь вид:
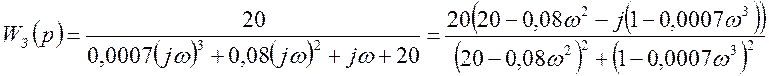 .
.
1.2 Расчет переходного процесса САУ
Получаем переходной процесс гораздо быстрее с помощью прикладной программы Mathсad.
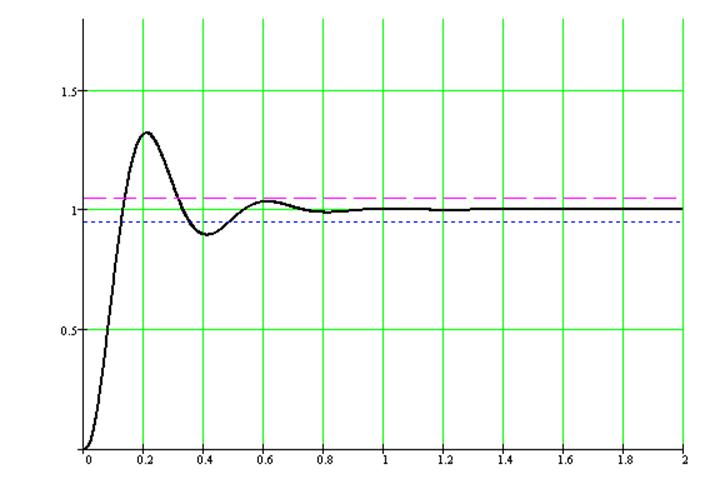
Рисунок 1.1 – Переходной процесс исходной АСР
По рисунку 1.1 определяются показатели качества. Коэффициент перерегулирования:
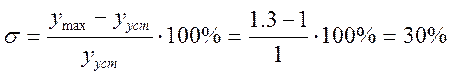
Время регулирования:
![]()
1.3 Расчет точности системы
Рассматриваем зависимость изображений ошибки Е(р) в функциях ∆х (р) и ∆F(р) :
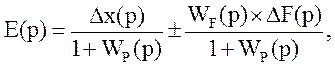
Первое слагаемое определяет ошибку по управляющему воздействию, а второе - по возмущающему.
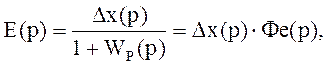
Разложив передаточную функцию Фе(р) в ряд по возрастающим степеням комплексной величины р, который сходится при малых значениях р, то есть при достаточно больших значениях времени t, что соответствует установившемуся режиму, выражение:
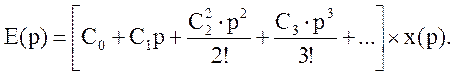
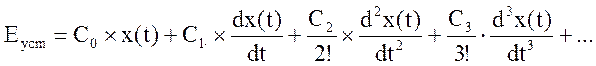
Величины Со, С1, С2, С3, ... называются коэффициентами ошибок и определяются по формулам :
![]()
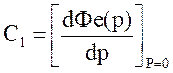
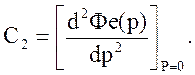
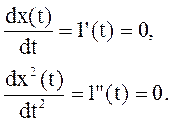 Производные задающего воздействия
будут следующими
Производные задающего воздействия
будут следующими
Запишем передаточную функцию замкнутой системы по ошибке :
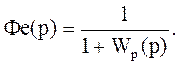
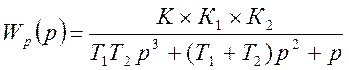 =
= 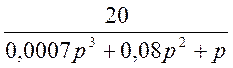
тогда
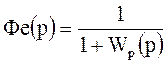 =
= 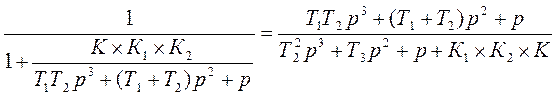 .
.
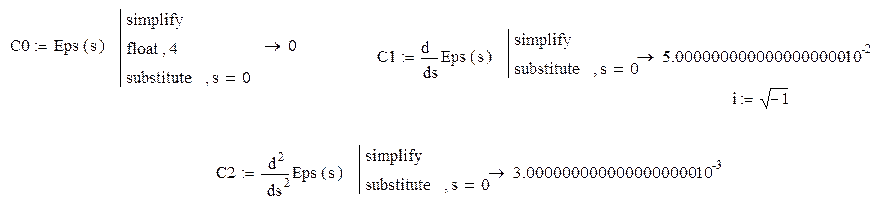
Значение ошибки в установившемся режиме определяется по формуле:
Еуст = Со × х(t) + С1 × х'(t) + С2 × х"(t) = 0 × 1 + 5 × 10-5×0 + 3×10-4 × 0 = 0
2. АНАЛИЗ УСТОЙЧИВОСТИ ИССЛЕДУЕМОЙ АСР
2.1 Критерий Гурвица
Для определения устойчивости АСР по критерию Гурвица необходимо использовать знаменатель выражения (1.2), то есть характеристическое уравнение системы в замкнутом состоянии.
Критерий устойчивости Гурвица сводится к тому, что при а0 > 0 должны быть положительными все n определители Гурвица, получаемые из квадратной матрицы коэффициентов. Уравнения (2.1) третьего порядка (n = 3) и для него получаем условия:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.