Синтез системы регулирования с использованием последовательной коррекции, страница 2

а₀ > 0,  ∆₁ = а₁ > 0, ∆₂ =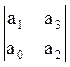 > 0

Третий (последний) определитель ∆₃ = а₃×∆₂, что дает условие а₃ > 0. Условие ∆₂ > 0 при а₀ > 0, а₁ > 0 и а₃ > 0 может выполняться только при а₂ > 0.

Найдем значение определителей:

∆₁ = а₁ = 0,08 > 0

∆₂ =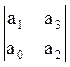 = а₁ ×а₂ - а₀ ×а₃ = 0,08×1 – 0,0007×20 = 0,066 > 0

а₀ = 0,0007 > 0,

2.2 Исследование устойчивости с помощью критерия Михайлова

Критерий Михайлова – это частотный критерий, основанный на рассмотрении кривой, определяемой характеристическим уравнением замкнутой системы. Запишем характеристическое уравнение  замкнутой системы, заменив оператор Лапласа на оператор Фурье:

Выделим действительную и мнимую составляющие:

         С помощью MathCAD, изменяя частоту от 0 до бесконечности, построим зависимость от (рисунок 2.1).

         По критерию Михайлова для того чтобы система была устойчива необходи­мо, чтобы вектор, характеризующий замкнутую систему регулирования, при из­менении частоты описывал в положительном направлении (не изменяя направле­ния) угол (где n - степень характеристического уравнения).

         Из рисунка наглядно видно, что вектор проходит последовательно в положительном направлении три квадранта (система третьего порядка) нигде не петлял и не обращаясь в ноль - следовательно, система устойчива.

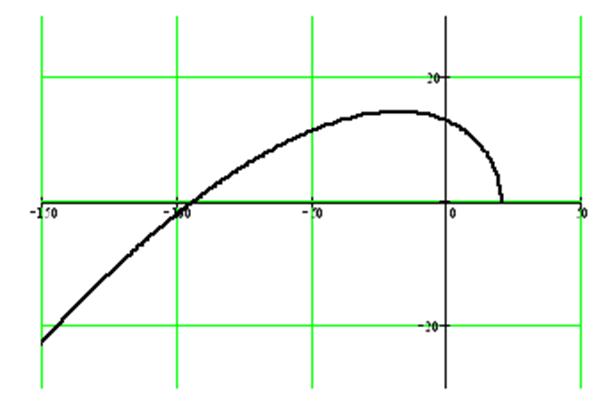
Рисунок 2.1 – Кривая Михайлова для характеристического уравнения третьего порядка

3. ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК

 Если на вход заданной системы подать синусоидальное воздействие           X_вх(ω) = А(ω)×sinωt, то на ее выходе в установившемся режиме, будет

 X_вых(ω) = А(ω)×sin(ωt + φ(ω)),                                  (3.1)

          Уравнение (3.1) – это амплитудно-фазовая частотная характеристика системы. Если заменить оператор Лапласа на оператор Фурье в выражении 1.2, то можно получить уравнение амплитудно-фазовой характеристика системы.

.

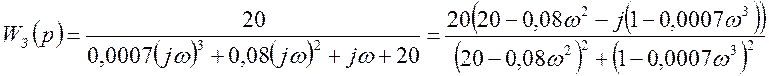Выделив в последнем выражении вещественную и мнимую часть, получим:

W(jω) = P(ω) + j × Q(ω),

Построение частотных характеристик осуществим с помощью прикладной программой Mathсad при изменении ω от 0 до ∞ (рисунки 3.1 – 3.3).

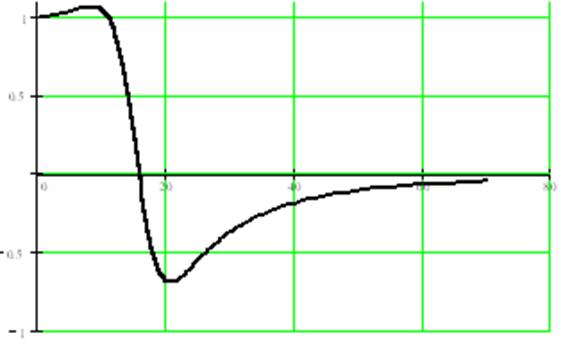
Рисунок 3.1 – Вещественная частотная характеристика

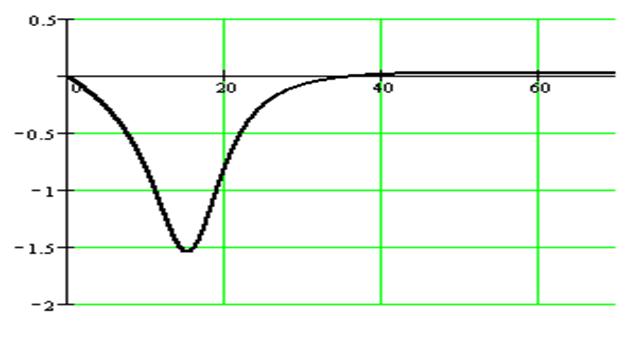
Рисунок 3.2 – Мнимая частотная характеристика

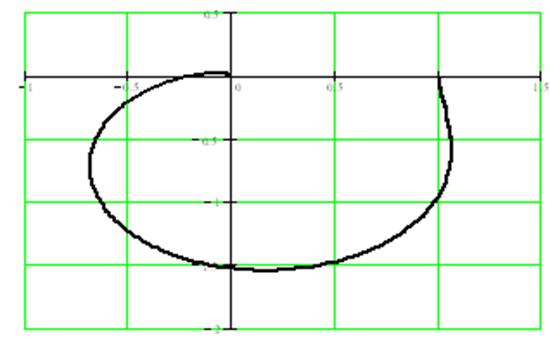
Рисунок 3.3 – Фазо -  частотная характеристика

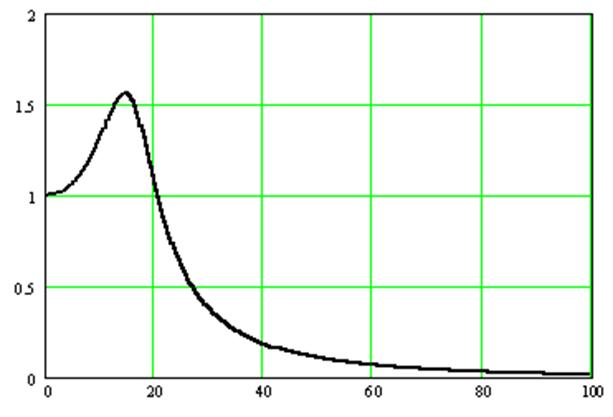
Рисунок 3.4 – Амплитудно – фазовая характеристика

W(jω) = A(ω) × φ(ω) = A(ω) × e^jωt = P(ω) + j × Q(ω),

          Таким образом, P(ω) = A(ω) × cos(ωt), а Q(ω) = A(ω) ×sin(ωt).

          Также иногда производится запись амплитудно-фазовой характеристики в показательной форме:

W(jω) = A(ω) × e^jωt,

A(ω) = = .

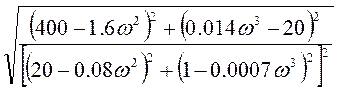                                                     φ(ω) = arctg =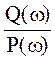

 = arctg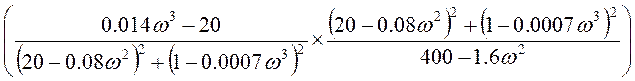

Изменяя частоту ω от 0 до ∞ в выражениях (3.3) и (3.4) при помощи прикладной программы Mathcad строим характеристики системы, представленные на рисунках 3.4 и 3.5

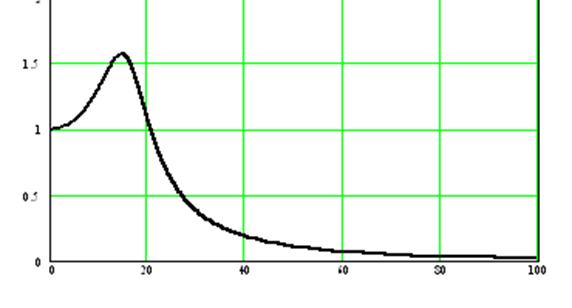
Рисунок 3.5 – Амплитудно-частотная характеристика

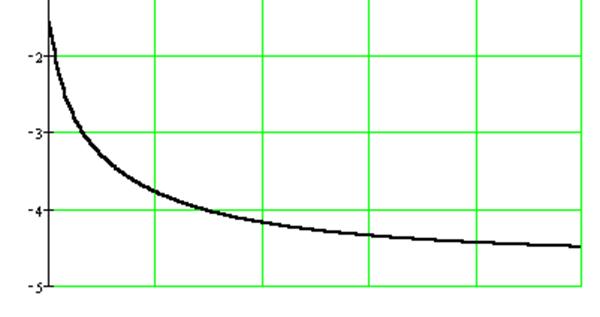
Рисунок 3.6 – Фазо-частотная характеристика

Для построения логарифмической амплитудно-частотной характеристики (рисунок 3.6) необходимо определить усиление амплитуды выходного сигнала по формуле:

L(ω) = 20lg KK₁K₂ – 20lg(ω) – 20lg– 20lg,

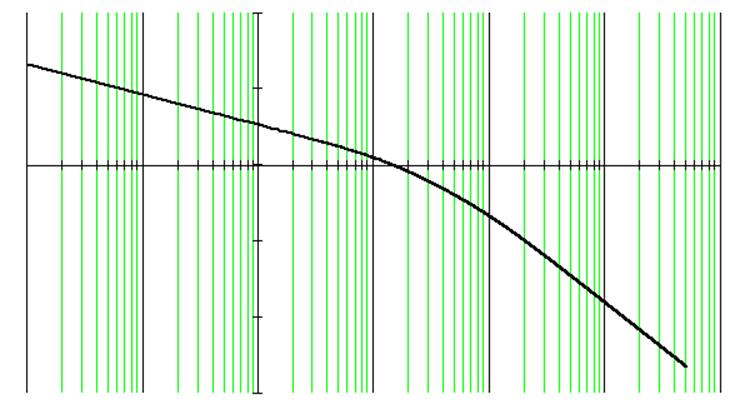
Рисунок 3.6 – Логарифмическая амплитудно-частотная характеристика

Для построения логарифмической фазо-частотной характеристики (рисунок 3.7) в полулогарифмическом масштабе по оси ординат откладываем фазу, вычисленную по формуле:

φ(ω) = - - arctg(T₁×ω) - arctg(T₂×ω).

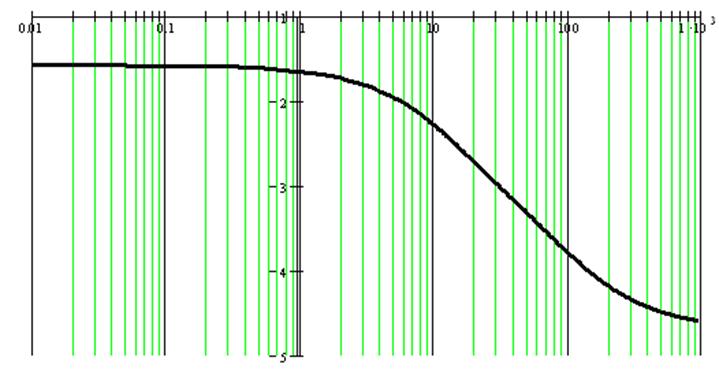
Рисунок 3.7 -Логарифмическая фазо-частотная характеристика

          4 СИНТЕЗ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

          4.1 Построение располагаемой ЛАХ

         

          Под располагаемой ЛАХ понимается характеристика исходной системы регулирования Обычно под исходной системой понимается система, состоящая из регулируемого объекта и регулятора и не снабженная необходимыми корректирующими средствами, обеспечивающими требуемое качество регулирования.

          По заданию имеем систему, состоящую из последовательно включенных интегрирующего и апериодического звеньев.

         На основании передаточной функции разомкнутой системы для такой системы справедливо:

       Найдем частотысопряжения:

ω_c1 = = = 100 с^-1;                        ω_c2 = = = 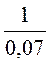14.2 с^-1.

        До первой частоты сопряжения будет действовать интегрирующее звено, что на рисунке соответствует наклонной -20 дБ/дек. На участке между частотами сопряжения имеем наклон -40 дБ/дек, третий участок ЛАЧХ имеет наклон                            -60дБ/дек. ЛАЧХ приведена на рисунке 4.1.

        4.2 Построение желаемой ЛАХ

 Построение желаемой ЛАХ производится в трёх областях (низкочастотной, среднечастотной и высокочастотной) по заданным показателям качества: величине

перерегулирования и времени регулирования:

              

         Исследователями  установлено,  что  при  частоте  среза  наклон  ЛАЧХ должен быть - 20 дБ/дек, а частота  определяется требуемым временем  переходного процесса и допустимым  перерегулированием.

        Для определения  воспользуемся номограммой, представленной на рисунке 6.40(2)

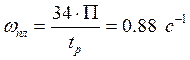
        По номограмме, указанной выше находим :

         Зная  можно определить  :

        Запасы устойчивости по амплитуде и фазе можно определить с помощью номограммы на рисунке 6.41(2).

         Желаемая ЛАХ приведена на рисунке 4.1

Рисунок 4.2 - Принципиальная схема корректирующего  устройства                       

Согласно виду логарифмической характеристики запишем передаточную функцию:

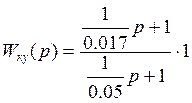
Чтобы определить параметры схемы, один из них необходимо задать. Принимаем С=20 мкФ. Тогда

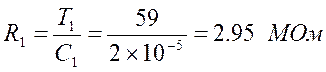
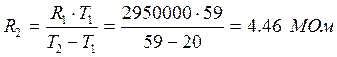
Найдем передаточную функцию скорректированного устройства:

W_р^ск(р) = .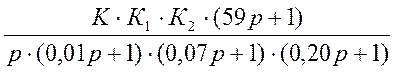

Построение переходного процесса скорректированной АСР проведем с помощью прикладной программы Mathcad. Полученная переходная характеристика скорректированной системы приведена на рисунке 4.3.

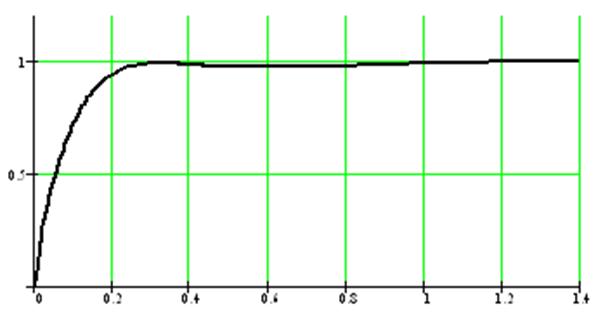
 Рисунок 4.3 - Переходный процесс скорректированной АСР

Таким образом, последовательное корректирующее устройство улучшило показатели качества. Получили: to = 0,25 и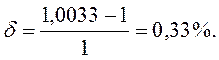

ЗАКЛЮЧЕНИЕ

В ходе данной курсовой работы были приобретены практические навыки по исследованию систем автоматического регулирования и их синтеза. Заданная система была проверена на устойчивость по критерию Михайлова.

Для этой системы рассчитали методом логарифмических частотных характеристик последовательное корректирующее устройство, которое должно обеспечивать:

                                to = 0,25 и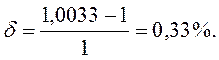

ПЕРЕЧЕНЬ  ССЫЛОК

1.  А.А. Иванов «Теория автоматического правления и регулирования»  - М., Недра, 1970 г.-351с.

2.  В.А. Бесекерский, Е.П. Попов «Теория систем автоматического регулирования»  - М., Наука, 1975 г., 768 с.

3.  Попов Е. П. «Теория линейных систем автоматического регулирования и управления»  - М., Наука, 1989 г.-301с.

4.  Теория автоматического управления и регулирования. /Под редакцией В.А. Нетушило/.- М., Наука, 1987 г., 400 с.