параметров, часто находящихся в противоречии друг с другом. С увеличением размерности пространства переменных, как правило, возрастают объем вычислений и сложность алгоритмов, а также затрудняется анализ поведения целевой функции.
3.1. Основные понятия линейной алгебры
Будем рассматривать функции многих переменных f(x)~ f(xlt...9xn) как функции, заданные в точках х «-мерного евклидова пространства Е„ : / = /О). Точки х е Е„ представлены векторами-столбцами координат x = (x],...,xj ("7" - знак транспонирования). Перечислим основные определения и понятия из курса линейной алгебры, которые будут использованы в дальнейшем.
В пространстве Еп возможны операции:
- сложения х + у = (xj + хн + уп);
- умножения на действительное число ;а-(Х\'1;...,/а"„)Де/е;
я
- скалярного произведения (х, у) = 2^х}ys ;
- определение длины (нормы) вектора х
- вычисления расстояния между векторами х и у
V ./=1
- для норм произвольных векторов х,у е Е„ справедливо неравенство треугольника ii- . vl!<|UU!Ul
lb
- скалярное произведение оценивают по модулю неравенством Коши-Буняковского
IMN4IHI.
Основные понятия, связанные с числовыми матрицами.
|
А = |
Матрица А = \ftg\i = 1,...,т: / = !,...,« представляет собой прямоугольный массив чисел, состоящий из m строк и п столбцов. Таким образом, вектор-столбец х является матрицей хп1.
a2i;a22;...;a2tl
Матрица А1 = (#,,), которая получается из матрицы А = {аи), если поменять местами ее строки и столбцы, называется транспонированной по отношению к матрицей.
Квадратная матрица А называется симметрической, если АТ = А. Матрицы одинакового размера А - (а&) и £=(&») можно складывать: А+В = {а{. +Ьи).
Результатом умножения матрицы А на число X является матрица: ЯА - уЦу).
Произведением Ах матрицы А = щ) размером m х п на вектор-столбец х 6 Еп называется вектор-столбец ЬеЕП1, координаты которого вычисляют по формуле
./=1
где а' ={an,...,alnf - вектор коэффициентов z-й строки матрицы А.
Для матриц A-{fly) и B = (hkl) соответственно размером /;? х п и п х т определено произведение АВ — С — {са), где элемент са матрицы С размером m х г находят из равенства
17
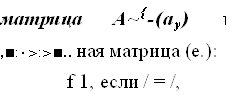 и
и
1>*А
Можно показать, что
Если рассматривать /7-мерные векторы-столбцыхи_у как матрицы размером «х 1, то формулу для их скалярного произведения можно получить по правилу умножения матриц х и у
Для каждой невырожденной матрицы А существует обратная
................. ,(-1 \ ... 4-\ , , ,-| ,.
= Е, где £ - единич-
если / /,
Элементы обратной матрицы могут быть найдены по форму-
II
(х,у)^х7 -у = (хи...,х„)
Уп
Заметим, что для х и у е Е„ произведение х • у задает квад-ратную матрицу
|
х1 |
• ад |
|||
|
... |
||||
|
- |
- -ад |
Если ,4 - квадратная симметрическая матрица размером п х я, то для любых векторов х и yeEtl (Ах, у) - {х, Ау), так как
{Ас, .у) = (Л*У> = х'А'у = Уф = {.г, ф).
Каждой квадратной матрице размером п х п можно поставить в соответствие число - определитель матрицы А (обозначается del А или \А\), которое находят по формуле
и
delA = \A\ = Y*aA =1
где A-,j - алгебраическое дополнение элемента а$ определяется соотношением
4,.=(-1ГХ>
где /Цу - минор, т.е. определитель матрицы, полученный из матрицы А вычеркиванием г'-й строки и /-го столбца.
Квадратная матрица называется вырожденной, если ее опре-цсли гель равен нулю, и невырожденной в противном случае.
ле
А.
(X:
u del А 9
где Ар - алгебраическое дополнение элемента ау, матрицы А. Пусть А ~ \а&) - симметрическая матрица размером п х п. То-
я п гда функция п переменных h},...,hfh Q.(h)=J^jaljhihl. = (Ah7h)
Ы jml
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.