Промышленность \ Физикохимия и механика композиционных материалов

Методы оптимизации композиционных систем, страница 20

При проектировании и оптимизации следует пользоваться достаточно точными и надежными, но в то же время и простыми моделями. Это требование объясняется тем, что в процессе принятия оптимального решения приходится неоднократно рассчитывать напряженное состояние конструкции и проверять выполнение критериев прочности. Критерии прочности должны быть применимы при сложном напряженном состоянии и допускать возможности варьирования структуры армирования материала. Из этого следует, что величины пределов прочности при сложном напряженном состоянии должны быть представлены как функции концентрации включений и связующего материала, их пределов прочности, ориентации волокон в монослоях. Задача эта чрезвычайно сложная. Поэтому при оптимизации часто ограничиваются использованием приближенных моделей прочности. Обычно принимают следующие упрощения:

1. Критерий разрушения отождествляется с условием локальной прочности. Это означает, что прочность консфукции считают исчерпанной, если хотя бы в одной точке определенная функция напряжении превысит предельное значение. Не рассматривают распространение зоны повреждений, не изучают


вопросы приспособляемости и предельной несущей способности.

2.  Задачу определения прочности исследуют в статической постановке.

3.  Композит считают сплошной средой, макроскопические характеристики которой зависят от свойств материала на микроуровне. Коэффициенты, фигурирующие в этих критериях прочности, вычисляют с помощью микроскопических теорий разрушения.

Далее рассмотрим некоторые несложные микроскопические механизмы разрушения и конструирование на их основе достаточно простого, но универсального критерия прочности.

8.2.1. Прочность волокнистых композитов при продольном растяжении вдоль волокон

Простейшая модель, используемая в расчетах на прочность, основана на следующих допущениях:

-  волокно и матрица несут нагрузку, пропорциональную их жесткости;

-  деформации растяжения в обоих компонентах равны, т.е. волокно и матрица деформируются совместно.

V,

(8Л2)

а.

Разрушение наименее прочного компонента приводит к разрушению композита и оно возникает, когда растягивающее напряжение достигает величины

<7| | = mm

г.

V, + — V ■     F

Более реальными являются оценки прочности однонаправленных композитов, состоящих из хрупких волокон. Прочность волокон характеризуется некоторым статистическим распределением. Считают, что прочность материала определяется накоплением разрывов волокон, разрушающихся независимо друт от друга. Роль матрицы сводится к локализации разрушения в пределах неэффективной длины волокна, так что разрыв волокна не приводит к полному выключению его из работы. Средняя прочность пучка волокон, расположенных в матрице со средней концентрацией V г,

5£=r>/fe)rw,                                    '                               (8-13)

где    в ~ 2.72;

а,р - параметры, связанные со средней плотностью волокна неэффективной длины /;


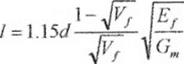
F

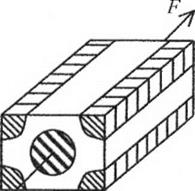
Рис. 8.8. Схема одноосного растяжения волокнистого композита


8.2.2. Прочность волокнистых композитов ори продольном сжатии вдоль волокон

Величина напряжения —— соответствует несимметричной фор-



ана~,ГГ°СТИ ПРИ                                                                      ВДишюг выражениями,

ст,

и

Ko-

к» +

/и

mi !

аналогичными оценкам при растяжении

/г..

mm

(8.14)

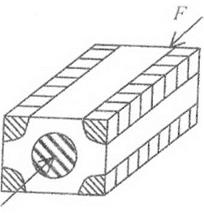
Рис. 8.9. Схема одноосного сжатия волокнистого композита

Более точные значения предела прочности при сжатии получают, если учитывают потерю устойчивости волокон. Критическое напряжение в композите, при котором происходит потеря устойчивости.

ме потери устойчивости, а  \—~- EmEf - симметричной. Теоре\   ^ m

тически предсказанная величина ах\ превосходит экспериментально измеренные значения примерно вдвое.

8.2.3. Прочность волокнистых композитов при поперечном растяжении и сдвиге


Для оценки прочности применяют модели, основанные на рассмотрении правильных периодических укладок волокон.

Скачать файл