Методы оптимизации композиционных систем, страница 15

вписывая в первый столбец таблицы А экспоненты при переменных в первом члене, во второй - экспоненты при переменных во втором члене и т.д. Таблица А чисел называется матрицей экспонент позинома (7.1).

Например, матрицей экспонент приведенного позинома g, является строка

4 =

Тогда соответствующий им позином можно записать в виде

/         \           1      2     1   1    2

g(x,y,z)=x + -yz +-xz + -y z.

7.2. Двойственная функция и двойственная задача

Для каждой задачи геометрического программирования может быть сформулирована так называемая двойственная задача, решение которой находится в самой тесной связи с решением

исходной задачи. Теория этих вопросов называется теорией двойственности.

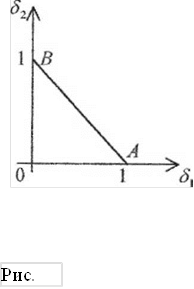
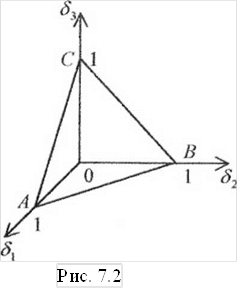
Пусть дан некоторый позином жащих на отрезке АВ (исключая концы) (рис. 7.1). При т = 3 это будет множество точек (<^,^₂,^₃), принадлежащих треугольнику ABC, исключая его стороны (рис. 7.2), и т.д.

т      а      а

Рассмотрим функцию т положительных переменных 8_У > 0,...Д„ > 0, определенную равенством

(7.4)

\⁸к)

Функцию                      называют двойственной функцией (по отношению к позиному gfo ,.-,*„))• Подчеркнем, что числа с_х,...,с_т в выражении двойственной функции u(S_x,...,S_m) - это коэффициенты позинома g(x_l9...₉x„). Кроме того, экстремальные свойства двойственной функции и позинома связаны самым тесным образом.

Рассмотрим задачу:

найти max u(S_x,..., 8_т) при условии, что

$><>,...,*. >о;                                                                                             (⁷-⁵)

Д+&+... + $.=!.                                                                     (7-6)

Таким образом, требуется найти такую точку (<?,",...,симплекса Q., которая определяет максимум двойственной функции

max^V..,<0 = ^,V-,^).

Эту задачу решают с помощью простой теоремы. Теорема 7.1. Наибольшее значение двойственной функции (7.4) на симплексе Q равно М = с, +...+ c_w и достигается в точkq(c₁/M,c₂/M,...,cJM)gQ:

Множество Q точек (S_l9...,S_m) (иначе - наборов из т действительных чисел £,,...ДД удовлетворяющих ограничениям (7.5) и (7.6), называется в математике т-мерным открытым симтепсом. При т = 2 это будет множество точек (S_US₂), ле-54

^Q                         try       \M    M

\