Методы оптимизации композиционных систем, страница 4

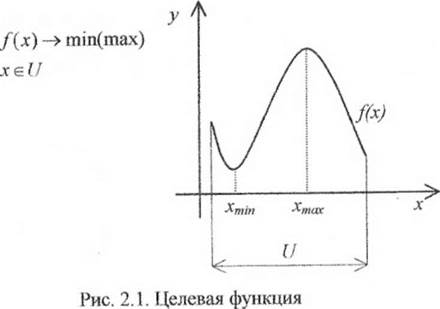
5.  Формулировка математической задачи оптимизации. Объединяя результаты предыдущих этапов построения математической модели, ее записывают в виде математической задачи оптимизации, включающей построенную целевую функцию и найденные ограничения на управляемые переменные. В достаточно общем виде математическую задачу оптимизации можно сформулировать следующим образом: минимизировать (максимизировать) целевую функцию с учетом ограничений на управляемые переменные. Под минимизацией (максимизацией) функции п переменных f(x) = f(x_l,...,x_il) на заданном множестве U п - мерного векторного пространства Е„ понимают определение хотя бы одной из точек минимума (максимума) этой функции на множестве U, а также, если это необходимо, и минимального (максимального) на U значения/ft).

6. Информационное обеспечение математической модели. Математическая модель, даже адекватная реальному объекту и достаточно полно отражающая его свойства, может оказаться бесполезной для практического использования, если отсутствует необходимая информация о величинах, параметрах, переменных, входящих в эту модель. Таким образом, в процессе построения математической модели объекта оптимизации необходимо следить за тем, чтобы значения всех входящих в нее величин могли быть измерены.

Пример 2.1

Математическое моделирование оптимизации проекта оросительного канала.

1. Определение границ объекта оптимизации. Считаем, что выбор пути, по которому будет проложен канал, диктуется внешними условиями (рельеф, расположение населенных пунктов и т.д.) и оптимизации не подлежит. Таким образом, оптимизация должна относиться только к форме и размерам поперечного сечения канала, которые полностью определяются шириной бетонных плит / и углом наклона <р его боковых стенок к плос-

кости дна. Сужение границ объекта оптимизации может быть связано с тем, что в проекте используют стандартные плиты заданной ширины lo I. Существенным обстоятельством считают только пропускную способность канала.

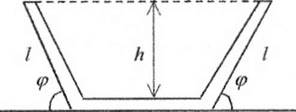
Рис.2.2. Поперечное сечение канала

2. Выбор управляемых переменных. Все характеристики поперечного сечения канала полностью определяются величинами / и (р. В данном случае управляемой переменной является угол

ср.

3. Определение ограничений на управляемые переменные. Из рисунка видны возможные пределы изменения угла д>

0<<р<-2

При (р = — поперечное сечение канала превращается в квадрат, а при дальнейшем увеличении (р конструкция становится неустойчивой. Под пропускной способностью канала W мы будем понимать объем воды, проходящей через его поперечное сечение в единицу времени

W = S-V, где S - площадь поперечного сечения; V- скорость воды (const);

S = /²(l + cos^)sin<p

W = K/²(l + cos#>)sin ф > W_min

4.   Выбор числового критерия оптимизации. Единственной целью оптимизации системы является обеспечение наибольшей пропускной способности канала W. Оптимальной ситуации соответствует максимум величины W, и числовым критерием оптимизации является целевая функция одной переменной

f((p) = VI² (\ + cos#>)sin (р,

которую следует максимизировать.

5. Формулировка математической задачи оптимизации.

/ (<р) = K/²(l + cos^jsin (р —> max

д<®<-2

6.   Информационное обеспечение математической модели. Построенная математическая модель содержит величины V и U, значения которых предполагаются известными. Отсутствие информации о хотя бы одной из них не позволит использовать данную модель для оптимизации проекта на практике.

Таким образом, в дальнейшем решение этой задачи сводится

(  я~\

к отысканию максимума функции f((p) на интервале (ре. 0;— .

3. Методы безусловной оптимизации функций многих переменных

Задача оптимизации композиционных материалов сводится н поиску экстремума функции многих переменных, поскольку создание любого нового материала треб ус i учет пс< кольни? cm

IS