Методы оптимизации композиционных систем, страница 19

Таким образом, получены более строгие оценки для эффективного модуля, чем оценки (8.4) и (8.5). Для оценок (8.6) справедливы следующие неравенства:

/*_и<//<//₍₊₎.

8.1.3. Композиты с волокнистыми наполнителями

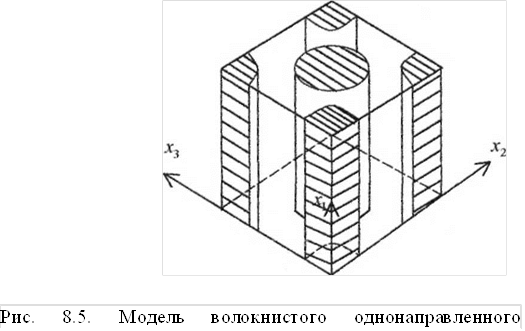Волокнистый композит моделируется системой однонаправленных параллельных прямолинейных волокон, уложенных в матрицу (рис. 8.5). Волокна представляют собой цилиндры, и материал можно считать двумерным аналогом гранулированного композита. Обычно волокна располагаются в поперечной плоскости случайным образом, и поэтому композит оказывается изотропным в поперечной плоскости.

Для линейно-упругих тел справедлив закон Гука

Ft

ES '

где F - продольная сила; / - длина тела; S - поперечное сечение; Е - модуль Юнга; d - удлинение тела.

Для двухфазного композита закон Гука записывают следующим образом:

s - gig ■

^13  .

2G

^ди             E₂₂    Е_ш

о - °23 23 ~~

^ЛН                      ^22                    ^22

где v - коэффициент Пуассона; Е - модуль Юнга; G = р - модуль сдвига; а - среднее напряжение; s - средняя деформация.

Индексы 11, 12,13 относятся к продольным, а 22, 23, 33 - поперечным упругим постоянным.

Кроме того, используют постоянную к - объемный модуль упругости при плоском деформированном состоянии

Ж^ЙЯЕ ^{МОДСЛЬ П}°~ *™ь еще две

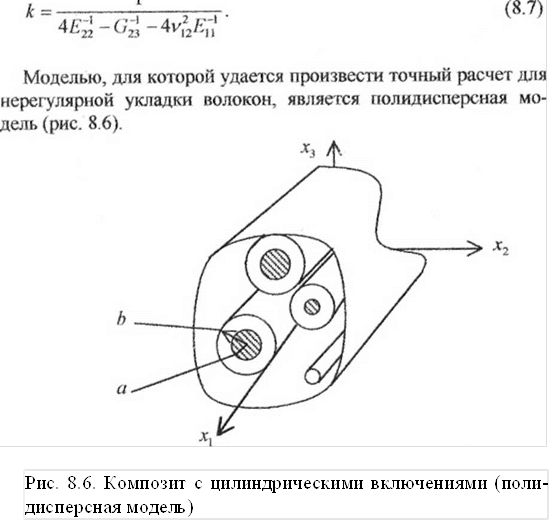
Это двумерный аналог пространственной полидисперсной модели, рассмотренной в предыдущем разделе. Волокна представляют собой бесконечно длинные круговые цилиндры, заключенные в непрерывную матрицу. С каждым волокном радиусом а связана оболочка радиусом Ъ из материала матрицы. В промежутках помещаются волокна все уменьшающегося диа°¹²=°~ ⁺ (в,-оУ₊У_я(20_тГ'

Для модуля сдвига G₂₃ в плоскости волокон в рамках поли-дисперсной модели можно установить лишь верхнюю и нижнюю границы.

Отметим один точный результат. Рассмотрим композиционный материал, образованный периодической укладкой изотропных волокон треугольного поперечного сечения в матрицу (рис. 8.7).

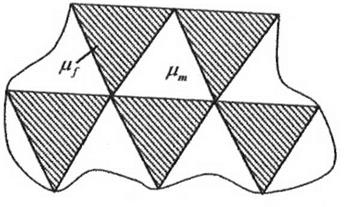
Рис. 8.7. Повторяющаяся структура композита при гексагональной упаковке волокон

Области, занятые материалом волокон и матрицы, представляют собой равносторонние треугольники, у которых объемные доли фаз совпадают и равны 0.5. Такой материал называется ставленного материала

Другое точное решение получено Хиллом для случая, когда модули сдвига фаз равны G_m - G_f - G. Тогда

V_m{k_f+G)+V_f(k_m + G)

Структуру волокнистых композитов можно регулировать периодической укладкой идентичных волокон в неограниченную упругую матрицу. В такой постановке необходимо найти решения краевых задач теории упругости с периодическими условиями на ячейке, а затем произвести усреднение напряжений и деформаций по объему элементарной ячейки.

8.2. Критерии прочности композиционных материалов

Проблемы неупругого поведения и, в частности, разрушения и прочности композитов не исследованы в настоящее время с достаточной полнотой и детальностью. Причиной такого положения является разнообразие физических явлений, обусловленных нелинейными эффектами поведения материала. Существует множество видов разрушения, усталости и потери несущей способности, как на уровне отдельных структурных элементов материала, так и конструкции в целом. По-разному разрушаются композиты при растяжении, сжатии, сдвиге в плоскости слоя и межслойкой деформации. Известны, по крайней мере, три возможных механизма разрушения при растяжении: распространение трещины в матрице, множественные разрывы волокон вследствие накопления повреждений и из-за объемного растрескивания слабейшего компонента. Разрушение материата при сжатии происходит из-за потери устойчивости волокон или в результате исчерпания прочности матрицы. При развитии зон неупругого поведения материала происходит сложная эволюция форм разрушений; обширные зоны множественного растрескивания порождают крупную "магистральную" трещину; потеря устойчивости отдельных слоев приводит к общему расслоению конструкции и т.д. Анализ прочности усложняется из-за высокой чувствительности материала к некоторым видам повреждений и несовершенств. Кроме того, адекватные математические модели физических процессов разрушения сложны и многообразны и не всегда рассматриваемые с их применением задачи решают доступными средствами.