Пример 6Л. Решить задачу
/(х) = х,2 + (х, - 4)2 -> min, х2 -х, -2<0 2х2~х2<0
методом штрафных функций.
Запишем последовательность вспомогательных задач минимизации
|
2х2-х, |
/,(х) = xf + (х2 -4f + к ■ У(х)У + к ■ [g;(xjf -> min,
™ g,+ = |(х2 -х, - 2 + |х2 - х} - 2|), g2+ == |(2х2 -х,2 +
В табл. 6.1 приведены решения этих задач для некоторых к.
Таблица 6.1
|
к |
xf |
А |
|
0 |
0 |
4 |
|
1 |
0.66 |
3.33 |
|
5 |
0.91 |
3.09 |
|
1.0 |
0.95 |
3.05 |
|
100 |
0.995 |
3.004 |
Точное решение задачи х = (l;3). Геометрическая иллюстрация приведена на рис. 6.3.
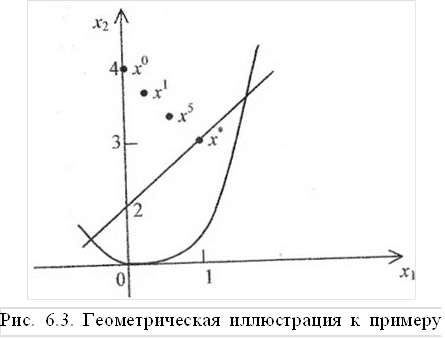
Замечания.
1. В качестве критерия останова в методе штрафных функций можно использовать неравенство |х* - хк/21 < £, где е > 0 - параметр точности; к - четное число. При его выполнении полагают х* = хк ,f* = f(xk).
2. Для оценки точности решения, полученного методом штрафных функций, можно использовать следующий факт. Пусть - - какая-либо внутренняя точка допустимого множества U задачи выпуклого программирования /(л')-> min, #,(*)< 0,i; = ],...,т (т.е. g,(z)<0 при всех/), а х - решение k-й вспомогательной задачи (6.5). Тогда справедлива следующая двухсторонняя оценка минимального значения функции f(x) на множестве U
ду)</</И, где хк - akz + (l - ак рск, а ак - наименьшее из значений ae[0;.l], при которых g.(az + (l -а)хк)< О для всех i = 1,..., т.
3. Недостатком метода штрафных функций является плохая обусловленность вспомогательной минимизируемой функции fk(x) при больших/:.
6.2.2. Метод барьерных функций
В этом методе исходная задача нелинейного программирования также сводится к последовательности задач безусловной минимизации (6.5), но функции (рк (х) выбирают таким образом, чтобы при больших к функции fk(x) из (6.5) мало отличались от
f(x) во внутренних точках х допустимого множества U и, в то же время, при приближении точки х е U к границе множества U эти функции неограниченно возрастали.
Последовательность функций {<рк(х)}, определенная во всех внутренних точках множества U, называется последовательностью барьерных функций этого множества, если выполняются условия:
1. lim<pk(х) = О для любой фиксированной внутренней точки к—хо х множества U;
2. \im(pk{xr)=+сю для любой последовательности \х'') внутренних точек множества О, сходящейся к какой-либо граничной точке этого множества.
Таким образом, влияние барьерной функции (рк{х) при больших к состоит в создании "барьера" с крутыми склонами вдоль границы допустимого множества.
 Пусть {Вк} - какая-либо числовая
последовательность с положительными членами и Vim Вк = 0, а функция q>(x) определек—><п на во всех внутренних точках множества U и стремится к + со при приближении точки х к границе множества (I. Тогда последовательность (рк(х)= Вк(р(х) является последовательностью барьерных функций.
Пусть {Вк} - какая-либо числовая
последовательность с положительными членами и Vim Вк = 0, а функция q>(x) определек—><п на во всех внутренних точках множества U и стремится к + со при приближении точки х к границе множества (I. Тогда последовательность (рк(х)= Вк(р(х) является последовательностью барьерных функций.
На практике часто полагают Вк = ~,к = 1,2,....
Если допустимое множество V задачи нелинейного программирования определяется системой неравенств
£,(*)< О, / = 1,...,ш, то в качестве функции (р(х) можно взять, например, т 1
*<*)—Е-гт (610)
Тогда вспомогательная функция fk(x) аз (6.5) принимает вид
At-K/t*)4x4v t6.ii)
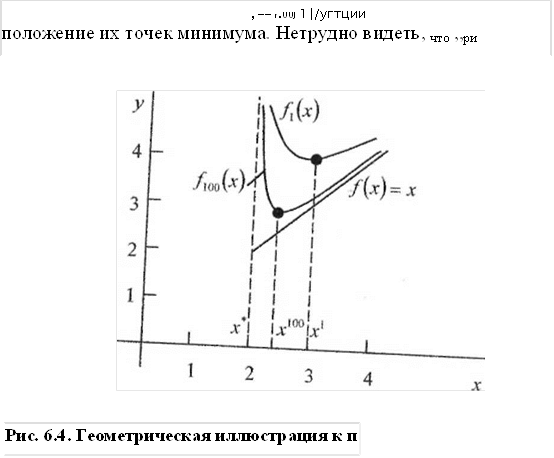
Хотя метод барьерных функций используют в задачах многомерной минимизации, рассмотрим для наглядности иллюстрацию этого метода в одномерном случае.
Пример 6.2. Решить задачу
/(*)= х ~» min, -*+2<0 методом барьерных функций, используя Циюиз(б.Ю).
Рассмотрим последовательность
|
х + |
зации
11
к х~2
|
х1 =3 |
й5 ГГ0ЛЬЙ°Й Т°ЧКИ ДОП~™ множества например х =5, найдем ее значения при различных к:
|
римеру 6.2 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.