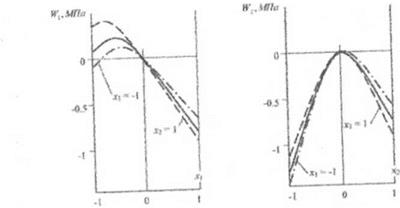
Промышленность \ Физикохимия и механика композиционных материалов

Методы оптимизации композиционных систем, страница 28

Рис III. Однофакторные зависимости предела прочности W от количества пластификатора х, и отвердителя х2 при квази-однофакторных моделях

tea

о--------------------------

-V. б

Рис  112 Зависимости оптимальной концентрации пласз и фикатора xLopl и отвердителя xZopt при различных уровнях стабилизации второго фактора

При подстановке, в частности, (11.3) в модель можно получить закономерности изменения прочности под влиянием индивидуального фактора Х|, но при условии, что другой фактор х2 будет поддерживаться на переменном оптимальном уровне (например, с помощью автоматического регулятора с прямой связью между X] их2):

3.177-0.494л-, -0.373л-,2.                                      (11.4)

Вместо прямой подстановки те же модели можно получить, используя общие формулы прироста эффектов за счет перевода х{ на оптимальный переменный уровень xlJSXt (11.1):

Aft,, = -0.25ft,2 lba; Aft,. = -0.5ЛД lb,, 1 Aft,, = -0.25ft,2 /ft,,; Aft,, = -0.%ft„">«■)

Для xlopl расчет приростов

AbQ = -0.25 x (- 0.48)2 /(- 0.38) = 0.152; Ab2 = -0.5 x (- 0.48X- 0.18)/(- 0.38) =0.114; Ab22 ш -0.25 x (- 0.18)2 /(- 0.38) = 0.021

позволяет перевести модель прочности композита в параболу

яКчргЬ3.322 + 0.304x2 -1.199д£.                                            (11.6)

Доверительные интервалы показаны на рис. 11.2. Обращает на себя внимание сравнительно широкий доверительный Интерпол  для   оптимальной  дозировки пластификатора х1ор1. Это объясняется тем, что парабола (11.6) более "островершинна",

101


чем (11.4), так как уЬ2!1\>|^,|. Анализ рис. 11.2 позволяет принять более простую, чем (11.2) гипотезу х, opi = const, поскольку проведенная через х1 = -0.632 параллельная оси х2 прямая полностью укладывается в доверительный интервал в пределах |х2| < 1. Таким образом, с риском а = 0.2 на основе статистических критериев отклоняется гипотеза о влиянии расхода отвердителя на оптимальную дозировку пластификатора, но может быть сохранена гипотеза (11.3) о линейном снижении оптимальной добавки отвердителя с ростом дозировки пластификатора.

С инженерной точки зрения целесообразно оценить потери L (от английского lost) критерия качества при замене линейных регулировочных функций (11.2) и (11.3) на константы, равные свободным членам в этих функциях, т.е. средним х1ор1 в диапазоне |x,| < 1, что равносильно назначению в (11.1) всех Ьр - 0.

Последнее приводит к тому, что разность в двухфакторной модели прочности композита определяется лишь приростом АЬа

(И.5):

= 0.25^/6,)^ +0.5£foA/A,)v.-                                                   (П'7)

Расчет по (11.7) Л„{х,}= 0.021.г| и LR{x2}= 0.007х2 показал, что потери при отказе от оптимальных переменных уровней невелики, следовательно, могут быть приняты х.   =-0.5— - оптимольные постоянные дозировки обоих компонентов.

Библиографический список

1.  Сайфуллин PC. Физикохимия неорганических полимерных и композиционных материалов. -М: Химия, 1990. -240 с.

2.  Васильев В.В. Механика конструкций из композиционных материалов. -М.: Машиностроение, 1988. - 272 с.

3.  Баничук Н.В., Кобелев В.В., Рикардс Р.Б. Оптимизация mi с ментов конструкций из композиционных материалов. М.: Машиностроение, 1988. - 224 с.

4.    Лесин В.В., Лисовец Ю.П. Основы методов оптимизации М.:МАИ, 1995.-341 с.

5.  Бекишев Г.А., Кратко М.И. Элементарное введение в геометрическое программирование. -М.: Наука, 1980. - 143 с.

6.  Калинин В.А., Якунин В.И. Геометрическое моделирование технологического процесса намотки в производстве ЛА. -М.:МАИ, 1995.-67 с.

7.  Батищев Д.И., Львович Я.Е., Фролов В..Н. Оптимизация в САПР. -Воронеж: Издательство ВГУ, 1997.-416 с.

8.  Вознесенский В.А., Ляшенко Т.В., Иванов ЯЛ, Нико-лов И.И. ЭВМ и оптимизация композиционных материалов. -Киев.: Будивэльнык, 1989.   240 с.

Скачать файл