Коэффициенты ![]() (некоторые
их них могут быть равны нулю) определяются параметрами звена (коэффициент
передачи, постоянные времени и пр.).
(некоторые
их них могут быть равны нулю) определяются параметрами звена (коэффициент
передачи, постоянные времени и пр.).
![]()
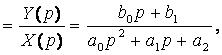
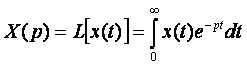
–
изображение входного воздействия x(t), ![]() – оператор
преобразования Лапласа.
– оператор
преобразования Лапласа.
![]()
Аналитическое выражение для функции y(t) определяют путем обратного преобразования Лапласа:
![]()
![]()
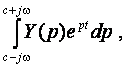
![]() – оператор, обратный оператору
Лапласа
– оператор, обратный оператору
Лапласа ![]() .
.
Таблица преобразований Лапласа для некоторых функций приведена в приложении.
Операторная форма записи дифференциального уравнения линейного звена:
![]()
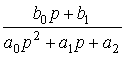
![]()
или
![]()
![]()
![]()
![]() –
оператор дифференцирования.
–
оператор дифференцирования.
![]()
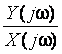
![]()
Графическое изображение функции ![]() на комплексной плоскости – амплитудно
- фазовая характеристика (АФХ) или годограф.
на комплексной плоскости – амплитудно
- фазовая характеристика (АФХ) или годограф.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.