Импульсные устройства. Основные понятия и определения импульсной техники. Электронные ключи. Интегральные логические схемы, страница 6

где  А- размах (амплитуда) экспоненты, а Б -  модуль разности асимптоты и выбранного уровня отсчёта. В простейшем случае рис.1.8в определим длительность фронта переходной характеристики  схемы рис.1.7, выбрав для отсчёта уровень : .Для определения интервала между двумя  уровнями применяют (1.13) дважды. Например, для определения длительности фронта как интервала между уровнями  и  получаем:    .

В завершение заметим, что возможно использование - цепочки таким образом, что выходное  напряжение снимается с резистора  (рис.1.7). Ясно, что изменения тока и напряжений при этом совершенно тождественны, а  цепочки условно называются интегрирующей и дифференцирующей.

1.3.2.  Переходные процессы в простейших злектрических цепях. Операторный метод

Широко распространённым  методом анализа переходных процессов является операторный метод (Лапласа), преобразующий дифференциальные уравнения в алгебраические. В терминах изображений  по Лапласу схему цепочки рис.1.7 можно представить в виде рис.1.9, где  изображение входного воздействия 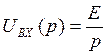   определяет действие источника , включаемого идеальным ключём  в момент времени . Изображение  тока в схеме рис.1.9 находится по уравнению Кирхофа

                                                         и изображение напряжения на конденсаторе

.                          (1.14)

Таким образом, (1.14) является изображением  выходного напряжения схемы при воздействии в виде скачка напряжения, т.е. изображением переходной характеристики . 

Рис. 1.9

Передаточная характеристика 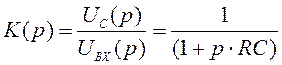 отличается от (1.14) множителем , соответствующим дифференцированию по времени, т.е. является изображением импульсной характеристики  при .

Для определения функции изменения во времени напряжения на конденсаторе  следует найти обратное преобразование Лапласа для .

В случае дробно-рационального выражения   эта процедура стандартна, проведём  её для рассматриваемого простого примера.

Знаменатель в (1.14) имеет два корня:   и .  Для выполнения обратного преобразования Лапласа представляют функцию  суммой простейших  дробей, знаменатели которых заданы разностью переменной  и корней знаменателя, например, для (1.14) :

,                                    (1.15)

где  - числовые коэффициенты (так называемые вычеты), обеспечивающие равенство выражений (1.14) и (1.15).  Полезность формы (1.15) состоит в том, что каждое слагаемое имеет известное обратное преобразование Лапласа в виде экспоненциальной функции ,  в результате чего общее напряжение представляется суммой экспонент

.                                         (1.16)  

Величины вычетов   определяются с  использованием  формулы обращения Хевисайда:

 ,                                    (1.17)

где множитель  сокращается с сответствующим множителем в знаменателе , определяющим полюс этого выражения. Для формулы (1.14)  получаем   ,,   , тогда  согласно (1.16):

.

Совпадение этого результата с (1.12)  демонстрирует эквивалентность анализа во временной и частотной областях. Выбор используемого метода определяется конкретной прикладной задачей.

1.3.3.Теорема об эквивалентном генераторе

При анализе электрических  цепей, в том числе и импульсных, неизбежным общим  вопросом является учёт параметров источника, воздействующего на цепь,  и параметров потребителя формируемых сигналов – нагрузки. Предположение  модели источника в виде, например, идеального генератора напряжения, требует или наложения ограничения на величину его внутреннего сопротивления, допускающего использование такой модели, или учёта действия этого сопротивления в составе анализируемой схемы. Аналогичная ситуация имеет место в отношении нагрузки, пренебрегать действием которой можно при достаточно высоком её сопротивлении (например, если используется вольтметр или электронный осциллоскоп с высоким входным сопротивлением). В противном  случае сопротивление нагрузки должно быть включено в схему разрабатываемого устройства и участвовать в расчётных соотношениях.