Импульсные устройства. Основные понятия и определения импульсной техники. Электронные ключи. Интегральные логические схемы, страница 16

В достаточно общем виде можно говорить о том, что структура цифровых устройств состоит из многочисленных ключевых элементов, соединённых  в последовательные и ветвящиеся цепочки, осуществляющие логические и арифметические операции над двоичными переменными. Поэтому имеет значение вопрос о преобразовании параметов переключения импульсных элементов при распространении операции переключения вдоль цепочки ключей  (рис.2.18).  Предполагая воздействие на первый ключ функции единичного перепада, определяем переходную характеристику (2.40) с учётом действия расмотренных факторов инерционности . В момент   перехода первой схемы в насыщение напряжение на её выходе  и  присоединённая к выходу ключа последующая схема начинает переходить из предполагавшегося насыщения в отсечку с параметрами переключения, рассмотренными в  2.2.2. Этот процесс снова допускает анализ в линейном режиме и возможность применения 

Рис. 2.18

схемы рис.2.16 в   для случаев нарастания и убывания выходного напряжения.

Свойства каждого последующего элемента цепочки рис.2.18 описываются такой же переходной характеристикой, однако на вход  поступает уже не единичный перепад, а функция . Для определения выходной переменной  можно использовать метод Лапласа и определить передаточную характеристику двух звеньев как произведение передаточных характеристик  и . Ясно, что число вычетов и число экспоненциальных слагаемых в результате удвоится. При дальнейшем увеличении числа ключей в цепочке усложнение задачи может создать проблемы даже при компьютерном анализе.

Используем анализ во временной области, основанный на вычислении свёртки входного воздействия с импульсной характеристикой:

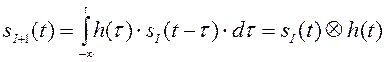,                 (2.41)

где    - импульсная характеристика элементов на рис.2.18.

Вычисление свёртки производится единственным оператором  (например,   в пакете Матлаб),  и его последовательное применение

Рис. 2.19

позволяет получить наглядное представление о преобразовании параметров переключения в цепочке. На рис.2.19 показано применение оператора свёртки к последовательности из девяти элементов на рис.2.18, переходные характеристики которых заданы по (2.40).

Для удобства сравнения будем расматривать только положительные функции  при переходах  и в насыщение, и обратно. Все каскады имеют постоянные времени  и   относительных единиц.

Переходная характеристика первого ключа совпадает с рис.2.17, имеет длительность фронта  по уровням  0,1-0,9  примерно  и запаздывание . Прохождение каждого последующего каскада вносит в переходную характеристику  дополнительное запаздывание, близкое к величине ,  т.е. инерционные свойства схем-нагрузок проявляются также, как действие монтажной ёмкости на рис.2.16, 2.17. 

Длительность фронта  возрастает достаточно интенсивно при прохождении первых 3-4 –х переключающих элементов, однако, начиная с 7-10 – го элементов увеличение практически прекращается и длительность фронта устанавливается на уровне,  близком к трём длительностям фронта одиночного ключа:

.                                                 (2.42)

Полученный результат имеет важное значение при оценке временных параметров цифровых устройств, состоящих из цепочек переключающих элементов. При этом считается, что в цепочке действует импульсный сигнал со стационарной длительностью фронта,  оцениваемой утроенной постоянной времени базового элемента при используемой технологии изготовления (2.42). В то же время в цифровой схеме возникает временная задержка, прямо пропорциональная  количеству элементов в цепочке :

.                                  (2.43)

Эта величина влияет на основные показатели цифрового устройства, такие как максимальная частота переключения, способы синхронизации и др.  и поэтому является основным показателем быстродействия импульсных схем.  Длительность фронта (2.42) представляет относительно меньший интерес и обычно в технических показателей цифровых элементов не участвует. Например, в пакете моделирования Orcad  быстродействие импульсных элементов моделируется просто как временная задержка ступенчатой функции.

2.2.6.  Ненасыщающиеся транзисторные ключи