Импульсные устройства. Основные понятия и определения импульсной техники. Электронные ключи. Интегральные логические схемы, страница 14

2.2.4.   Переходный процесс, определяемый действием коллекторно-базовой ёмкости

Вторым фактором, влияющим на динамические показатели транзисторного ключа, является коллекторно-базовая ёмкость , входящая вместе с граничной частотой 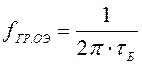  в паспортные данные транзистора. Характерное свойство действия   состоит в том, что эта ёмкость связывает выходную и входную  цепи ключа,  осуществляя  этим обратную связь. На рис.2.14 показана схема транзисторного ключа с учётом действия .

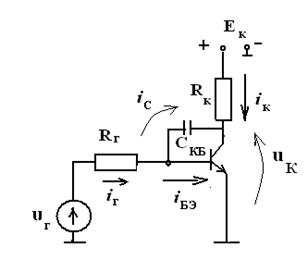
  Рис. 2.14

При подаче на вход ступенчатого воздействия  возникает ток 

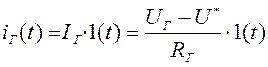.                            (2.32)

В активном режиме транзистора по мере заряда диффузионной ёмкости (рис.2.7) с постоянной времени  нарастают базовый и коллекторный токи , в результате чего уменьшается напряжение на коллекторе транзистора     и возникает  ток через коллекторно-базовую ёмкость:

 .  (2.33)

Этот ток согласно рис.2.14 ответвляется от тока генератора , чем   уменьшает ток базо-эмиттерного перехода , что в свою очередь уменьшает скорость нарастания базового и коллекторного  токов. Таким образом ёмкость  осуществляет отрицательную обратную связь и является причиной замедления процесса переключения транзистора между отсечкой и насыщением (или обратно).

Обобщённое описание действия обратной связи

При  всём многообразии использования обратных  связей  существует общее соотношение, связывающее свойства передаточных функций системы с обратной связью и при её отсутствии. На структурной схеме рис.2.15 обозначены:  - входная и выходная переменные системы с обратной связью, - глубина обратной связи,   - переменная обратной связи  и 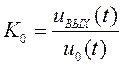  - коэффициент усиления без обратной связи. 

По умолчанию предполагается отрицательная обратная  связь, поэтому  переменная на входе усилителя   при включении обратной связи образуется вычитанием  .  Тогда передаточная функция системы                                                                                             .                            (2.34)

Формула (2.34) обладает общностью , поскольку применима к переменным любой физической природы, в частности,  к напряжениям или токам при соответствующем определении  функции обратной связи . 

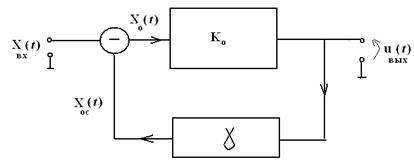
Рис.2.15

Во многих практических применениях    обратная связь используется при . Тогда  в знаменателе (2.34) можно пренебречь единицей и определить, что свойства системы с обратной связью определяются только свойствами цепи обратной связи.

                                                                                              .   (2.35)

Такая независимость  от свойств усилителя  оказывается весьма полезной во многих применениях, поскольку при микроэлектронной технологии изготовления параметры  могут очень мало зависеть от дестабилизирующих факторов любого свойства: температуры, влажности, радиации и др.

Отметим также, что (2.34) применима и для положительной обратной связи (), если . Однако при этом  превышает коэффициент усиления усилителя  и благоприятное свойство стабильности (2.35) утрачивается.  При   коэффициент передачи обращается в бесконечность и система с положительной обратной связью становится неустойчивой к действию сколь угодно малых помех.

            Переходная характеристика ключа с учётом действия .  Переменные в (2.34) могут быть вещественными функциями,  изображениями по Лапласу, преобразованиями Фурье и др.линейными преобразованиями переменных  ,.  Для анализа схемы рис.2.14 применим к (2.34) преобразование Лапласа и получим:

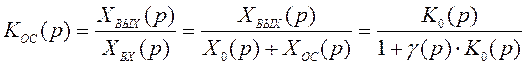
В схеме рис.2.14 в отсутствие  цепи обратной связи ступенчатый ток генератора (2.32) целиком попадает в базу транзистора     и токи базы и коллектора нарастают по экспоненте с постоянной времени :  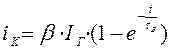.  Изображение по Лапласу этого тока:  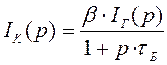.  Тогда передаточная функция по току транзистора без обратной связи равна:

 .                    (2.36) 

Ток в цепи обратной связи (рис.2.14)  протекает через ёмкость  и согласно (2.33) пропорционален производной по времени от коллекторного тока. Преобразуя (2.33) по Лапласу, получим: .  Тогда передаточная функция цепи обратной связи по току равна:

.

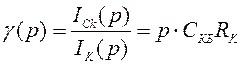Обозначим  и,  подставляя  и  в (2.34), получим: