Импульсные устройства. Основные понятия и определения импульсной техники. Электронные ключи. Интегральные логические схемы, страница 2

Способ отсчёта амплитуды импульса А  в условиях  неопределённой формы импульса  достаточно произволен и на рис.1.1 принят в области горизонтального участка вершины. 

Вторым важным параметром является длительность импульса . Можно условиться определять величину    на уровне половины амплитуды: 0.5 (рис.1.1).              Длительность  импульса определяет  возможное число передаваемых импульсов в единицу времени, т.е. представляет меру информативности импульсного сигнала. Поэтому история развития импульсной электроники фактически есть борьба за сокращение длительностей используемых  импульсов.

Существенное отличие формы импульса на рис.1.1 от прямоугольного состоит в наличии участков плавного нарастания и спада функции . Определение длительности этих участков обычно производят на уровнях от 0,1 до 0,9  от амплитуды А  и  называют  их длительностью фронта (rise time)  и спада (fall time).  Можно также ввести количественную меру прямоугольности импульса:

  .                                                            

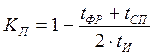При анализе свойств импульсных цепей для оценки вносимых искажений используют  специальные тестовые воздействия. При этом чаще всего используется функция Хевисайда, называемая также функцией единичного скачка (рис.1.2а):

       при      и      при .                             (1.1)   

Рис. 1.2

Реакция линейной электронной схемы на воздействие в виде единичного скачка напряжения или тока (1.1) называется переходной характеристикой . Эта характеристика является исчерпывающей, уникальной характеристикой исследуемой схемы и будет многократно использоваться в последующем материале.

С использованием функции Хевисайда легко построить модель прямоугольного импульса (рис.1.2 б):

,                                      где    - длительность импульса.

В математическом классе обобщённых функций в качестве воздействия на систему используется также  производная по времени от единичного скачка (1.1), называемая функцией Дирака:

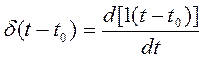.                                                      (1.2)

Реакция линейной системы на воздействие в виде функции называется импульсной характеристикой системы . Для линейной системы справедливо соотношение (1.2), в результате  переходная и импульсная характеристики связаны дифференциальной зависимостью:

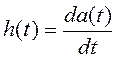 .                                                          (1.3)

Напомним, что наиболее общим свойством линейной системы является применимость принципа суперпозиции (наложения), состоящего в том, что реакция системы на сумму каких либо воздействий равна сумме реакций на эти воздействия, приложенные раздельно. Применяя это положение, получаем, что реакция линейной схемы на воздействие в виде прямоугольного импульса представляется  суммой переходных характеристик, вызываемых фронтом и спадом импульса (с соответствующей временной задержкой на время ).

1.1. Специальные виды импульсных сигналов

1.1.1.  Периодические сигналы

В ряде случаев используются периодические импульсные сигналы, повторяющиеся через заданный интервал времени  (рис.1.3).  В классических РЛС периодический характер сигнала открывает возможность накопления энергии повторяющегося сигнала и достижения таким образом желаемой дальности работы РЛС.

В современных электронных цифровых устройствах генераторы периодических импульсных сигналов играют  роль электронных часов, задающих масштаб времени достаточно сложного устройства (main generator, clock time). К таким генераторам предъявляются жёсткие требования по стабильности периода повторения. Обратим внимание на то, что на рис.1.3 импульсы существуют левее нуля (в отрицательном времени). Если импульсы появляются

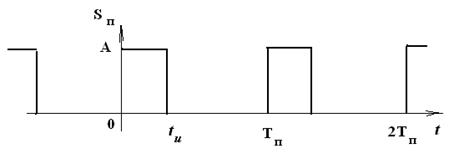
Рис. 1.3

только при , то имеет место не периодический сигнал, а включение последовательности периодических импульсов, сопровождающееся неизбежными переходными процессами.  

Обратную величину интервала повторения импульсов называют частотой повторения  (в англоязычной литературе – темп повторения (pulse repetition rate, PRR)). Существенной характеристикой периодических сигналов является соотношение периода повторения и длительности импульса, называемое  скважностью: