Модели импульсных устройств состоят из пассивных элементов: резисторов, конденсаторов и индуктивностей и ключевых элементов: транзисторов, диодов. Для обеспечения последующего изложения продемонстрируем несколько практических приёмов, используемых при анализе разнообразных схем.
1.3.1.Переходные процессы в простейших злектрических цепях. Анализ во временной области
Вначале
рассмотрим простейшую модель переходного процесса в ![]() цепочке,
управляемой источником напряжения
цепочке,
управляемой источником напряжения ![]() с помощью идеального
ключевого элемента
с помощью идеального
ключевого элемента ![]() (рис.1.7). Источник
(рис.1.7). Источник ![]() предполагается идеальным источником
напряжения, т.е.
предполагается идеальным источником
напряжения, т.е. ![]() . При анализе и испытаниях, а
также в технической документации, обычно устанавливают общую точку схемы
(«Земля»), относительно которой и определяют интересующие напряжения,
например, напряжение на конденсаторе
. При анализе и испытаниях, а
также в технической документации, обычно устанавливают общую точку схемы
(«Земля»), относительно которой и определяют интересующие напряжения,
например, напряжение на конденсаторе ![]() .
.

Рис. 1.7
Ёмкость ![]() как инерционный элемент описывается
линейным дифференциальным уравнением первого порядка:
как инерционный элемент описывается
линейным дифференциальным уравнением первого порядка:
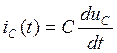 . (1.7)
. (1.7)
Согласно (1.7) переходный процесс
изменения напряжения на конденсаторе определяется интегралом от тока,
доставляющего заряд ![]() в ёмкость:
в ёмкость:
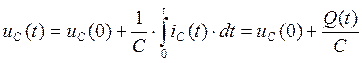 , (1.8)
, (1.8)
где ![]() -
напряжение на конденсаторе при
-
напряжение на конденсаторе при ![]() .
.
Для получения
переходной характеристики ![]() используем
скачкообразное изменение (1.1) управляющего напряжения
используем
скачкообразное изменение (1.1) управляющего напряжения ![]() ,
что в схеме рис.1.7 моделируется замыканием идеального ключа
,
что в схеме рис.1.7 моделируется замыканием идеального ключа ![]() . После замыкания ключа в схеме согласно
уравнению Кирхофа протекает ток
. После замыкания ключа в схеме согласно
уравнению Кирхофа протекает ток
 , (1.9)
, (1.9)
заряжающий конденсатор. Величина
тока в начальный момент максимальна  и уменьшается,
стремясь к нулю, по мере заряда конденсатора
и уменьшается,
стремясь к нулю, по мере заряда конденсатора ![]() .
Временная зависимость (1.9) как решение дифференциального уравнения (1.7)
выражается экспоненциальной функцией с постоянной времени
.
Временная зависимость (1.9) как решение дифференциального уравнения (1.7)
выражается экспоненциальной функцией с постоянной времени ![]() :
:
 . (1.10)
. (1.10)
На примере (1.10)
определим правило практического вычерчивания экспоненциальной зависимости
(рис.1.8а). Для этого, предполагая ![]() , при
, при ![]() фиксируем начальное значение
фиксируем начальное значение  и асимптотичекое
и асимптотичекое ![]() при
при ![]() (крестики
на рис.1.8а). Используем представление экспоненты степенным рядом
(крестики
на рис.1.8а). Используем представление экспоненты степенным рядом
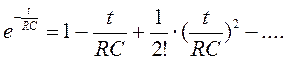 (1.11)
(1.11)
и, ограничиваясь двумя
слагаемыми, проведём штриховую линию, пересекающую ось времени в точке ![]() (кружок на рис.1.8а). Учёт трёх
параметров: начального и асимптотического значений и постоянной времени
обеспечивает вычерчивание диаграммы на рис.1.8а, количественно близкое к
точному значению экспоненциальной функции.
(кружок на рис.1.8а). Учёт трёх
параметров: начального и асимптотического значений и постоянной времени
обеспечивает вычерчивание диаграммы на рис.1.8а, количественно близкое к
точному значению экспоненциальной функции.
Известная величина
тока (1.10) позволяет определить в схеме рис.1.7 напряжение на резисторе: ![]() и по закону Кирхофа
и по закону Кирхофа ![]() - напряжение на конденсаторе (диаграммы
рис.1.8б,в):
- напряжение на конденсаторе (диаграммы
рис.1.8б,в):
![]() . (1.12)
. (1.12)
Зависимость ![]() представляет реакцию
представляет реакцию ![]() -цепочки рис.1.7 на супенчатое воздействие
-цепочки рис.1.7 на супенчатое воздействие ![]() , т.е. её переходную характеристику
, т.е. её переходную характеристику![]() . Выражение (1.12) демонстрирует
характерное «перераспределение» напряжения генератора между элементами
. Выражение (1.12) демонстрирует
характерное «перераспределение» напряжения генератора между элементами ![]() - цепочки, поэтому может быть более
наглядным, чем интеграл (1.8). Отметим, что при построении экспоненты
- цепочки, поэтому может быть более
наглядным, чем интеграл (1.8). Отметим, что при построении экспоненты ![]() постоянная времени
постоянная времени ![]() (кружок
на диаграмме) откладывается на линии асимптоты ( рис 1.8в).
(кружок
на диаграмме) откладывается на линии асимптоты ( рис 1.8в).
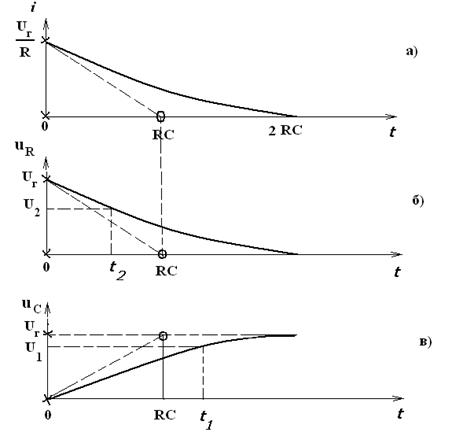
Рис. 1.8
При анализе
переходных процессов практический вопрос состоит в определении интервала
времени, требуемого для достижения некоторого уровня экспоненты. Например, по
диаграмме рис.1.8в требуется определить время ![]() , за
которое нарастающая экспонента
, за
которое нарастающая экспонента ![]() достигнет уровня
достигнет уровня ![]() . Подставляя
. Подставляя ![]() в
(1.12), получим уравнение относительно
в
(1.12), получим уравнение относительно ![]() , логарифмируя
которое, определим:
, логарифмируя
которое, определим: 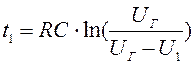 . Для убывающей экспоненты
. Для убывающей экспоненты ![]() и уровня
и уровня ![]() (рис.1.8б),
аналогичные выкладки приводят к соотношению
(рис.1.8б),
аналогичные выкладки приводят к соотношению 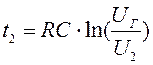 . В
обоих случаях в числителе под логарифмом стоит величина, равная разности
начального и асимптотического уровня (размах) экспоненты, а в знаменателе –
разность асимптотического уровня и выбранного уровня отсчёта. Поэтому для
нарастающих и убывающих экспонент при любом их знаке и смещении на постоянный
уровень действует общая формула:
. В
обоих случаях в числителе под логарифмом стоит величина, равная разности
начального и асимптотического уровня (размах) экспоненты, а в знаменателе –
разность асимптотического уровня и выбранного уровня отсчёта. Поэтому для
нарастающих и убывающих экспонент при любом их знаке и смещении на постоянный
уровень действует общая формула:
 , (1.13)
, (1.13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.