Введение в математический анализ. Дифференциальное исчисление функции одной переменной: Конспект лекций, страница 9

N M Рис. 21

– секущая. ОПРЕДЕЛЕНИЕ. Касательной к кривой в точке   называется предельное положение ее секущей  , когда точка , оставаясь на кривой, стремится к  (если такое положение существует) (рис. 21). Рассмотрим функцию  . Напишем уравнение касательной к  ее графику в точке

y y1             N                                         y0    M           О           x0    x1         x Рис. 22

– угол между MN и OX,   – угол между  касательной и OX (рис. 22). Будем искать уравнение касательной в виде , где  – угловой коэффициент прямой. – угловой коэффициент секущей.

Если , то , то есть  . Если  достаточно мало, то угловой коэффициент секущей   и равенство тем точнее, чем меньше . Можно утверждать, что

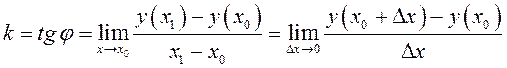
– угловой коэффициент касательной.

Так как при решении обеих задач (и не только их) пришлось выполнять  одни и те же действия, то для обозначения этих действий введем новое понятие.

ОПРЕДЕЛЕНИЕ. Производной функции  в точке  называется предел отношения ее приращения в этой точке к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю:

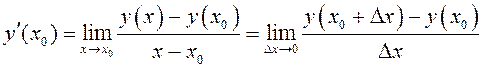
или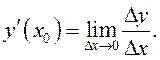                                               

Отсюда  – угловой коэффициент касательной к графику функции  в точке   Уравнение касательной  

Геометрический смысл производной: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке.

Физический смысл производной: производная функции в точке характеризует скорость ее изменения в окрестности этой точки. Отсюда следует, что если  то

Так как из определения следует, что производная в разных точках, вообще говоря, различна, то она сама является функцией.

ЗАМЕЧАНИЕ. Очевидно, для того чтобы функция имела производную, необходимо, чтобы она была непрерывной. Тогда   (определение 2 непрерывности), поэтому при вычислении производной по определению необходимо раскрыть неопределенность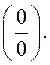 

ПРИМЕР. Вывести формулу вычисления производной функции  

По определению 

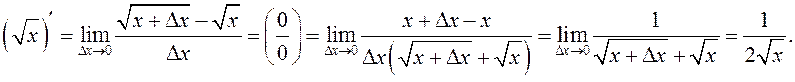
Так как  понятие производной связано с понятием касательной, то в тех точках, где график не имеет касательной, функция не имеет производной. Также ее нет в тех точках, где касательная к графику функции есть, но она перпендикулярна оси  OX.

y             х1    О     х2   х3  х4         х5          x Рис. 23

 не существует, так как предельные положения левой и правой секущих различны (рис. 23).

  не существует, так как предельное положение секущей в этой точке вертикально, то есть перпендикулярно оси OX (рис. 23).

– тупой). – острый), – угол между касательной и положительным направлением ОХ (рис. 23).

ОДНОСТОРОННИЕ ПРОИЗВОДНЫЕ

Введем понятия левой и правой производных функции   по аналогии с понятием левого и правого предела.

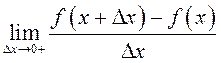ОПРЕДЕЛЕНИЕ. Правой производной функции  в точке  называется  при условии, что этот предел существует.

То, что  означает, что , то есть при вычислении правой производной   к точке  приближаются справа.

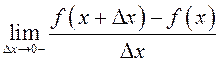ОПРЕДЕЛЕНИЕ. Левой производной функции  в точке  называется  при условии, что этот предел существует.

При вычислении левой производной  полагается .

Имеют место утверждения:

1. если  функция имеет в точке  производную , то она имеет в этой точке как левую, так и правую производные, причем 

2. если функция имеет в точке  как правую, так и левую производные, причем эти производные равны между собой, то в точке  существует производная, причем .

3.  если , то в точке  функция не имеет производной.

ПРИМЕР. Рассмотрим функцию  .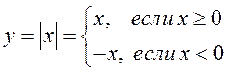

Вычислим односторонние производные (правую и левую) в точке .

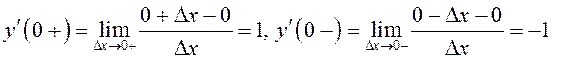. Односторонние производные неравны, значит,   не существует. В других точках эта функция производную имеет.    

ПОНЯТИЕ  ДИФФЕРЕНЦИРУЕМОСТИ.

ДИФФЕРЕНЦИАЛ ФУНКЦИИ