ОПРЕДЕЛЕНИЕ.
Точка ![]() называется точкой локального максимума
(минимума) функции
называется точкой локального максимума
(минимума) функции ![]() , если
, если ![]()
![]() Точки локального максимума или минимума
называются токами локального экстремума (или просто точками экстремума)
(рис.15).
Точки локального максимума или минимума
называются токами локального экстремума (или просто точками экстремума)
(рис.15).
|
x0 О x1 x2 x Рис. 15
|
ПРИМЕР. 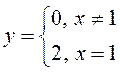
|
2 1-δ 1 1+δ x Рис. 16 |
точка максимума (рис. 16). |
ТЕОРЕМА (вторая теорема Вейерштрасса). Всякая непрерывная на отрезке функция достигает на этом отрезке своих наименьшего и наибольшего значений (без доказательства).
 y
y
![]()
![]()
a О b
х0
Рис. 17
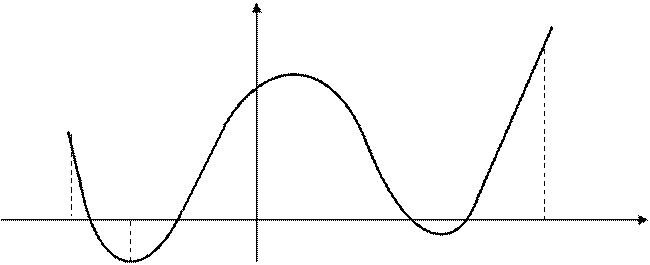
Как видно из рисунка 17, наибольшее и наименьшее
значения достигаются либо на концах отрезка, либо в точках
локального экстремума: ![]() точка минимума,
точка минимума, ![]() правый конец отрезка.
правый конец отрезка.
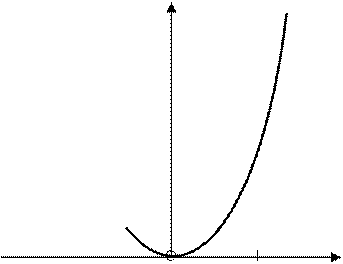 ЗАМЕЧАНИЕ. Непрерывная функция, заданная на интервале,
может не иметь ни наименьшего, ни наибольшего значений (рис. 18).
ЗАМЕЧАНИЕ. Непрерывная функция, заданная на интервале,
может не иметь ни наименьшего, ни наибольшего значений (рис. 18).
|
y
О 2 x Рис. 18 |
|
ТЕОРЕМА (Больцано
– Коши). Пусть ![]() непрерывна для всех
непрерывна для всех ![]() и
и ![]() Тогда
существует точка
Тогда
существует точка ![]() такая, что
такая, что ![]()
Геометрический
смысл этой теоремы ясно виден на
рисунках: перейти с верхней полуплоскости ![]() на
нижнюю
на
нижнюю ![]() , двигаясь вдоль графика непрерывной
функции, не пересекая ось
, двигаясь вдоль графика непрерывной
функции, не пересекая ось ![]() , нельзя (рис. 19, 20).
, нельзя (рис. 19, 20).
|
a c b x Рис.
19 |
a c4 b
Рис. 20 |
Без доказательства.
ТЕОРЕМА (о
промежуточных значениях). Пусть функция ![]() непрерывна
для всех
непрерывна
для всех ![]() и
и ![]() – ее
наименьшее и наибольшее значения соответственно. Тогда для любого значения
– ее
наименьшее и наибольшее значения соответственно. Тогда для любого значения ![]() найдется
найдется ![]() такое,
что
такое,
что ![]()
Теорема утверждает, что непрерывная функция принимает все промежуточные значения между своими наибольшим и наименьшим значениями.
ДОКАЗАТЕЛЬСТВО.
Рассмотрим ![]() , при этом
, при этом ![]() по
теореме 6. Пусть
по
теореме 6. Пусть ![]() Эта функция непрерывна при всех
Эта функция непрерывна при всех
![]() по теореме 1. Кроме того, очевидно,
по теореме 1. Кроме того, очевидно, ![]() Тогда для функции
Тогда для функции ![]() выполнены
условия теоремы 7, то есть существует точка
выполнены
условия теоремы 7, то есть существует точка ![]() такая,
что
такая,
что ![]() Что и требовалось доказать.
Что и требовалось доказать.
Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ,
ЕЕ ФИЗИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
К понятию производной приводят различные задачи из физики, механики, геометрии и других областей знания. Рассмотрим две такие задачи.
ЗАДАЧА О ВЫЧИСЛЕНИИ МГНОВЕННОЙ СКОРОСТИ. Пусть тело движется с переменной скоростью и ![]() – путь, пройденный за время
– путь, пройденный за время ![]() Определить мгновенную скорость в любой
момент времени
Определить мгновенную скорость в любой
момент времени ![]()
Если
к моменту времени ![]() пройдено расстояние
пройдено расстояние ![]() , а к моменту
, а к моменту
![]()
![]() – расстояние
– расстояние ![]() то
то 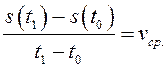 –
средняя скорость движения. Если
–
средняя скорость движения. Если ![]() – достаточно мало, то
– достаточно мало, то 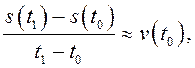 причем это приближенное равенство тем точнее,
чем меньше промежуток времени
причем это приближенное равенство тем точнее,
чем меньше промежуток времени ![]() , и если
, и если ![]() , то есть
, то есть ![]() , то
можно утверждать, что
, то
можно утверждать, что
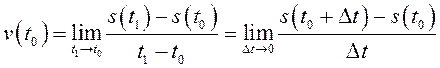
–
мгновенная скорость в момент ![]() .
.
ЗАДАЧА О ПРОВЕДЕНИИ КАСАТЕЛЬНОЙ
К ГРАФИКУ ФУНКЦИИ
Вначале дадим определение касательной к произвольной
кривой в некоторой ее точке (известное определение касательной к окружности
для произвольной кривой не подходит, например: ось ![]() имеет с
параболой
имеет с
параболой ![]() одну общую точку, однако касательной к ней
не является).
одну общую точку, однако касательной к ней
не является).
Секущей будем называть прямую, проходящую через две точки, лежащие на кривой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.