ОПРЕДЕЛЕНИЕ.
Функция ![]() называется дифференцируемой в точке
называется дифференцируемой в точке ![]() , если ее приращение в этой точке,
соответствующее приращению
, если ее приращение в этой точке,
соответствующее приращению ![]() , представимо в виде
, представимо в виде ![]() где
где ![]() а
а ![]() то есть
то есть ![]() – б.м.
функция в точке
– б.м.
функция в точке ![]()
ТЕОРЕМА (необходимое
и достаточное условие дифференцируемости функции) Для того, чтобы функция ![]() была дифференцируемой в некоторой точке
была дифференцируемой в некоторой точке ![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы ![]() имела в этой точке конечную производную
имела в этой точке конечную производную ![]() .
.
ДОКАЗАТЕЛЬСТВО.
1. Необходимость: ![]() существует
конечная производная
существует
конечная производная ![]() .
.
Если ![]() то
то 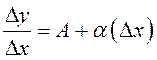 . Так как
. Так как ![]() , то
существует
, то
существует 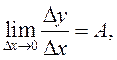 но по определению
но по определению 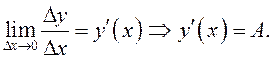
2.
Достаточность: существует конечная производная ![]()
![]() где
где ![]() – б.м.
в точке
– б.м.
в точке ![]()
Обозначим
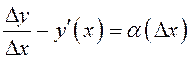 . По условию существует
. По условию существует 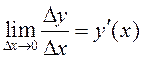 , поэтому
, поэтому 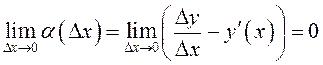 .
.
Тогда
![]() и если обозначить
и если обозначить ![]() ,
то теорема доказана.
,
то теорема доказана.
Таким образом, мы доказали, что дифференцируемость функции в некоторой точке эквивалентна существованию в этой точке конечной производной, поэтому процедуру вычисления производной называют дифференцированием.
|
aО x0 b x Рис. 24 |
|
Если ![]() дифференцируема в точке
дифференцируема в точке
![]() , то ее приращение в этой точке
, то ее приращение в этой точке ![]() состоит из двух частей:
состоит из двух частей: ![]() – линейная относительно
– линейная относительно ![]() и
и ![]() –
нелинейная относительно
–
нелинейная относительно ![]() , б.м. более высокого
порядка малости, чем
, б.м. более высокого
порядка малости, чем ![]() .
.
ОПРЕДЕЛЕНИЕ.
Дифференциалом функции ![]() в точке
в точке ![]() называется главная линейная часть ее
приращения в этой точке:
называется главная линейная часть ее
приращения в этой точке: ![]()
Если
![]() то
то ![]() поэтому
поэтому
![]() Принято считать, что если
Принято считать, что если ![]() – независимая переменная, то
– независимая переменная, то ![]() Итак, по определению
Итак, по определению ![]() .
.
ПРИМЕР. ![]() – найти
– найти ![]()
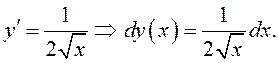
В частности 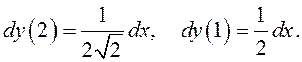
ТЕОРЕМА (о
связи непрерывности и дифференцируемости). Пусть функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , тогда она непрерывна в этой точке.
, тогда она непрерывна в этой точке.
ДОКАЗАТЕЛЬСТВО.
По определению дифференцируемости приращение функции ![]() представимо
в виде
представимо
в виде ![]() . Тогда
. Тогда ![]() , что
по определению 2 означает непрерывность
, что
по определению 2 означает непрерывность ![]() в точке
в точке
![]() .
.
ЗАМЕЧАНИЕ. Обратное утверждение неверно, то есть не всякая непрерывная функция дифференцируема (график непрерывной функции может иметь касательную не во всех точках).
ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ
ТЕОРЕМА (о
производной сложной функции). Пусть функция ![]() дифференцируема
в некоторой точке
дифференцируема
в некоторой точке ![]() , а функция
, а функция ![]() дифференцируема в соответствующей точке
дифференцируема в соответствующей точке ![]() , тогда сложная функция
, тогда сложная функция ![]() дифференцируема в точке
дифференцируема в точке ![]() и
и ![]() .
.
ДОКАЗАТЕЛЬСТВО.
Зададим ![]() Тогда функция
Тогда функция ![]() получит
приращение
получит
приращение ![]() (быть может
(быть может ![]() ), а
функция
), а
функция ![]() – приращение
– приращение ![]() Так как
функция
Так как
функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , то по определению
, то по определению ![]() где
где ![]() .
Разделим
.
Разделим ![]() на
на ![]() :
: 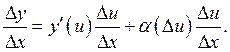 По условию
По условию ![]() дифференцируема,
значит,
дифференцируема,
значит, 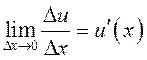 и
и ![]() по
теореме о связи непрерывности и дифференцируемости. Таким образом, если
по
теореме о связи непрерывности и дифференцируемости. Таким образом, если ![]() , то
, то ![]() Отсюда
имеем:
Отсюда
имеем:
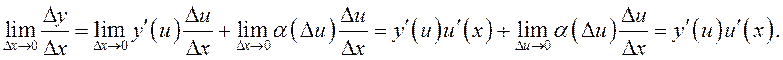
Итак, ![]() , что и требовалось
доказать.
, что и требовалось
доказать.
ПРИМЕР.
Найти производную функции ![]() .
.
Это
сложная функция: ![]()
Поэтому
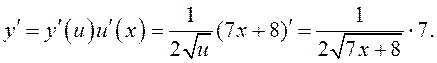
ДИФФЕРЕНЦИРОВАНИЕ ОБРАТНОЙ ФУНКЦИИ
ТЕОРЕМА (о
производной обратной функции). Пусть функция ![]() удовлетворяет
условиям теоремы о непрерывности обратной функции в некоторой окрестности точки
удовлетворяет
условиям теоремы о непрерывности обратной функции в некоторой окрестности точки
![]() , дифференцируема в этой точке и
, дифференцируема в этой точке и ![]() Тогда обратная функция
Тогда обратная функция ![]() дифференцируема в соответствующей точке
дифференцируема в соответствующей точке ![]() и
и 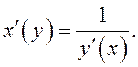
ДОКАЗАТЕЛЬСТВО.
Зададим приращение ![]() Так как по условию теоремы о
непрерывности обратной функции
Так как по условию теоремы о
непрерывности обратной функции ![]() и
и ![]() строго монотонны, то
строго монотонны, то ![]() Тогда
Тогда 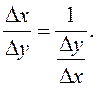 По
условию функция
По
условию функция ![]() дифференцируема, значит,
непрерывна, поэтому
дифференцируема, значит,
непрерывна, поэтому ![]() также непрерывна по теореме о
непрерывности обратной функции. Отсюда
также непрерывна по теореме о
непрерывности обратной функции. Отсюда ![]() (определение
2).
(определение
2).
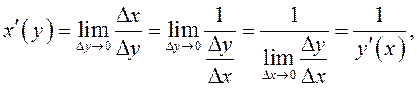 так как по условию
так как по условию ![]() дифференцируема
и
дифференцируема
и ![]() Что и требовалось доказать.
Что и требовалось доказать.
ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ,
ПРОИЗВЕДЕНИЯ И ЧАСТНОГО
ТЕОРЕМА.
Пусть ![]() дифференцируемы в некоторой точке
дифференцируемы в некоторой точке ![]() . Тогда их сумма, разность, произведение и
частное (при
. Тогда их сумма, разность, произведение и
частное (при ![]() ) также дифференцируемы в этой точке и
) также дифференцируемы в этой точке и
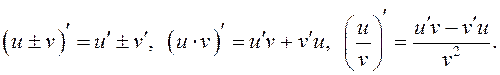
ДОКАЗАТЕЛЬСТВО.
Формулу ![]() вывести самостоятельно.
вывести самостоятельно.
Рассмотрим функцию ![]() .Зададим
приращение
.Зададим
приращение ![]() , тогда
, тогда
![]()
![]()
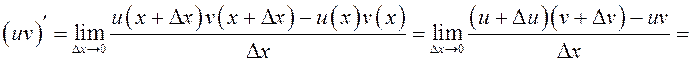
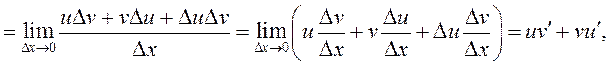
так
как ![]() дифференцируема по условию, значит,
непрерывна, а потому
дифференцируема по условию, значит,
непрерывна, а потому ![]()
Пусть 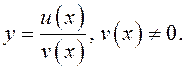
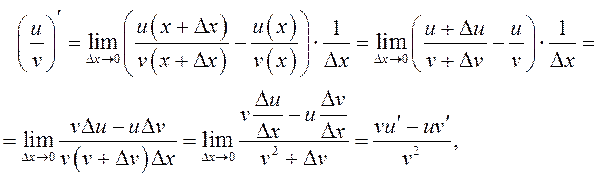
так
как ![]() по условию дифференцируема, значит,
непрерывна, а потому
по условию дифференцируема, значит,
непрерывна, а потому ![]() Что и требовалось доказать.
Что и требовалось доказать.
ТАБЛИЦА ПРОИЗВОДНЫХ
|
1. |
2. |
3. |
|
4. |
5. |
6. |
|
7. |
8. |
9. |
|
10. |
11. |
12. |
|
13. |
14. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.