Введение в математический анализ. Дифференциальное исчисление функции одной переменной: Конспект лекций, страница 7

ОПРЕДЕЛЕНИЕ. Элементарной называется всякая функция, которая задана одним аналитическим выражением, составленным из простейших элементарных функций при помощи четырех арифметических действий и суперпозиций, примененных конечное число раз.

ЗАМЕЧАНИЕ. Из доказанных теорем следует, что все элементарные функции непрерывны в области определения.

ПРИМЕРЫ. 1) 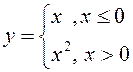  – элементарной не является, так как задана двумя аналитическими выражениями.

2) 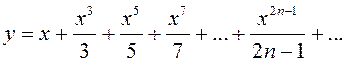  – элементарной не является, так как представляет собой сумму бесконечного числа слагаемых.

3) 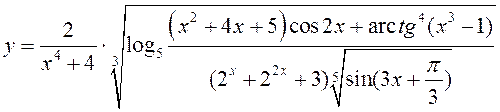  – элементарная функция, она непрерывна всюду, где определена.

Пусть   определена   Если каждому значению   (или соответствует единственное значение  , то говорят, что функция  – обратная для функции  .

y y x     О                   x Рис. 10

2)   – обратная функция определена и  (рис. 10).

3)   – обратная функция не существует. Но если рассматривать тольк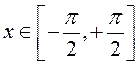о  , то  – обратная функция (рис. 11). Обратная функция существует также, если считать, например, что 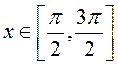  или 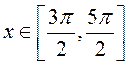  и т.д, так как одному значению   на каждом из этих промежутков соответствует единственное значение  .

y             1 О                                   x       -1           Рис. 11

y y 1 О    x                   x Рис.12

4)       Обратная функция  (рис.12).

Как видно из рассмотренных примеров, существование обратной функции  связано с монотонностью функции  .

ОПРЕДЕЛЕНИЕ. Функция   называется возрастающей (убывающей) на множестве Х, если

Возрастающие или убывающие функции называются строго монотонными.

ТЕОРЕМА (о непрерывности обратной функции). Пусть функция  непрерывна и строго монотонна на   и  Тогда на   (или на ) определена обратная функция , также непрерывная и строго монотонная.

ДОКАЗАТЕЛЬСТВО. Пусть, например,   возрастает на , то есть если  и  , то  Покажем, что   также возрастает, то есть  если  , то . Предположим противное:  Тогда, так как по условию   возрастает, то   что противоречит выбору  . Таким образом,   возрастает.                                         

Пусть  произвольно и такое, что .   (рис. 13). Так как   возрастает, то   

Выберем  так, что   Если  ,  то      , так как   тоже возрастает. Таким образом,  , что и означает непрерывность обратной функции.

ТЕОРЕМА (об устойчивости знака непрерывной в точке функции). Пусть   непрерывна в окрестности точки  и  тогда существует   такое, что      для всех 

Эта теорема имеет ясный геометрический смысл: если непрерывная функция положительна (отрицательна)  в точке  , то она положительна (отрицательна) и где-то рядом.

ДОКАЗАТЕЛЬСТВО. Пусть, например,   Так как   непрерывна в точке  , то по определению 2  предела функции в точке

Пусть       

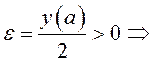
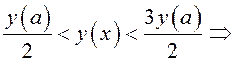
Случай   рассматривается аналогично с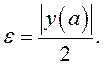   

ОПРЕДЕЛЕНИЕ. Функция  называется ограниченной сверху (снизу) на множестве , если   такое, что

Функция, ограниченная снизу и сверху, называется ограниченной на  , то есть

ТЕОРЕМА (первая теорема  Вейерштрасса). Всякая непрерывная  на отрезке функция ограничена на этом отрезке (без доказательства).

ЗАМЕЧАНИЕ. Непрерывная функция, заданная  на интервале, может быть неограниченной.

y 0,5 О                           2                              x Рис. 14

Очевидно,  то есть функция ограничена снизу, но сверху на этом интервале функция неограниченна (рис. 14).