ЗАМЕЧАНИЕ.
Если при отыскании наклонной асимптоты графика оказалось, что ![]() то график имеет горизонтальную асимптоту
то график имеет горизонтальную асимптоту ![]() (если
(если ![]() существует).
Если хотя бы один из пределов бесконечен или не существует, то график не имеет
ни наклонной, ни горизонтальной асимптот.
существует).
Если хотя бы один из пределов бесконечен или не существует, то график не имеет
ни наклонной, ни горизонтальной асимптот.
ПРИМЕР.
Найти асимптоты графика функции ![]()
Функция
определена ![]() , значит, вертикальных асимптот нет. Найдем
наклонные асимптоты.
, значит, вертикальных асимптот нет. Найдем
наклонные асимптоты.
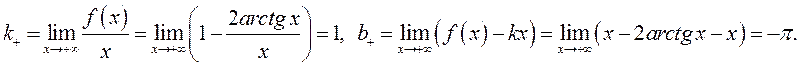
Таким образом, при ![]() –
наклонная асимптота.
–
наклонная асимптота.
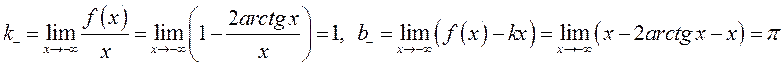 , откуда
, откуда
![]() – асимптота графика при
– асимптота графика при ![]()
Исследуем первую производную этой функции и построим эскиз графика (рис. 37).
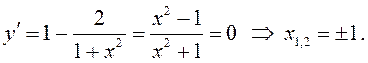
|
|
у
Рис. 37 |
ПРИМЕР.
Найти асимптоты графика функции ![]()
ОДЗ: 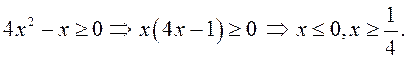
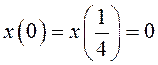 – вертикальных асимптот нет.
– вертикальных асимптот нет.
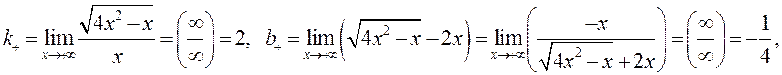
то есть при 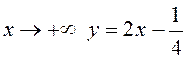 – асимптота.
– асимптота.
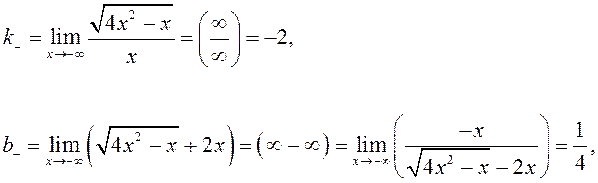
|
О Рис. 38 |
и
Эскиз графика этой функции имеет вид (рис.38): |
ПРИМЕР.
Найти асимптоты графика функции ![]()
Функция
определена ![]() , поэтому вертикальных асимптот нет.
, поэтому вертикальных асимптот нет.
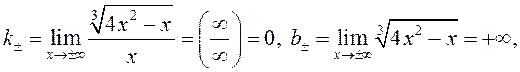
значит, график асимптот не имеет.
ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
И ПОСТРОЕНИЕ ЕЕ ГРАФИКА
1. Найти ОДЗ.
2. Определить свойства четности, нечетности, периодичности.
3. Найти точки разрыва и определить их характер.
4. Найти асимптоты графика.
5. Найти интервалы монотонности и экстремумы.
6. Определить направление выпуклости графика и точки перегиба.
7. Найти точки пересечения графика с осями координат.
8. Построить график: а) построить асимптоты б) отметить контрольные точки из пп.5,6,7
в) построить график слева направо, используя информацию из п.п.5, 6.
ЗАМЕЧАНИЕ.
Если ![]() – четная функция, то ее график симметричен
относительно оси
– четная функция, то ее график симметричен
относительно оси ![]() ; если нечетная, то симметричен
относительно начала координат. График периодической функции достаточно
построить на отрезке длиной в период, а потом периодически продолжить.
; если нечетная, то симметричен
относительно начала координат. График периодической функции достаточно
построить на отрезке длиной в период, а потом периодически продолжить.
ПРИМЕР.
Исследовать функцию 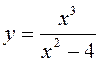 , построить ее график и эскизы
первой и второй производных .
, построить ее график и эскизы
первой и второй производных .
1. ОДЗ: ![]()
2. Функция нечетная, то есть график симметричен относительно начала координат.
3.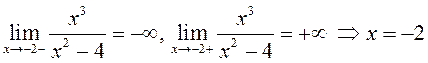 по определению точка
разрыва второго рода. Точку
по определению точка
разрыва второго рода. Точку ![]() можно не исследовать
вследствие нечетности функции и симметрии графика.
можно не исследовать
вследствие нечетности функции и симметрии графика.
4. ![]() –
вертикальные асимптоты. Наклонные асимптоты:
–
вертикальные асимптоты. Наклонные асимптоты:
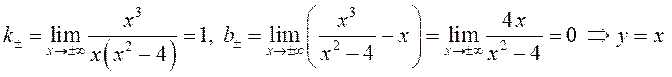
–
наклонная асимптота при ![]()
5. 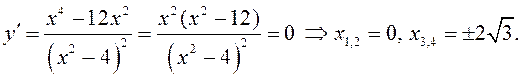
Исследуем функцию на монотонность и экстремумы (рис. 39).
|
max min
Рис. 39 |
![]()
6. 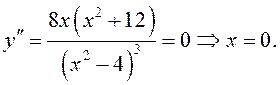
Определим направление выпуклости графика и точки перегиба (рис. 40).
|
точка перегиба
Рис. 40 |
![]() – точка перегиба.
– точка перегиба.
7. ![]()
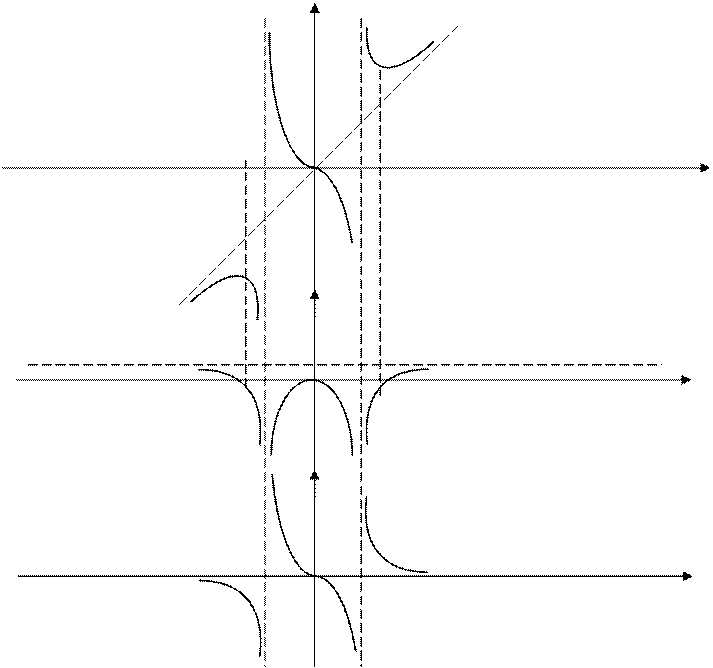 8. Построим
график, а по нему – эскизы
8. Построим
график, а по нему – эскизы ![]() и
и ![]() (рис. 41):
(рис. 41):
|
у -2 2 х
1 -2 2 х
х Рис. 41 |
Библиографический список
1. Кудрявцев, В.А. Краткий курс высшей математики / В.А. Кудрявцев, Б.П. Демидович. – М.: Наука, 1989.
2. Пискунов, Н.С. Дифференциальное и интегральное исчисление / Н.С. Пискунов. – М.: Наука, 1978. – Т.1.
3. Шипачев, В.С. Основы высшей математики / В.С. Шипачев. – М.: Высш. шк., 1998. – 200 с.
4. Шнейдер В.Е. Краткий курс высшей математики / В.Е.Шнейдер, А.И. Слуцкий, А.С. Шумов. – М.: Высш. шк. 1978. – Т.2.
.
Редактор
Компьютерная верстка
ИД 06039 от 12.10.01
Подписано в печать Формат 60х84 1/16
Бумага офсетная. Отпечатано на дуплекаторе.
Усл.печ.л. Уч.-изд.л.
Тираж экз. Заказ
Издательство ОмГТУ. 644050, Омск, пр-т Мира, 11
Типография ОмГТУ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.