Введение в математический анализ. Дифференциальное исчисление функции одной переменной: Конспект лекций, страница 12

y О                                      x Рис. 26

Если график функции имеет в точке экстремума касательную, то она параллельна оси ОХ (рис. 26).

ТЕОРЕМА (Ролля). Пусть функция   непрерывна  , дифференцируема    и  тогда существует   такая, что

y                                              aОbх Рис. 27

Геометрический смысл теоремы: если , то на графике дифференцируемой функции есть точки, в которых касательная параллельна оси ОХ (рис. 27).

ДОКАЗАТЕЛЬСТВО. Так как  непрерывна , то по второй теореме Вейерштрасса  она достигает  на  своих наибольшего  и наименьшего  значений либо в точках экстремума, либо на концах отрезка.

1. Пусть , тогда

2. Пусть  Так как  то либо , либо  достигается в точке экстремума , но по теореме Ферма   Что и требовалось доказать.

ТЕОРЕМА (Лагранжа). Пусть функция   непрерывна   и  дифференцируема   , тогда существует   такая, что  .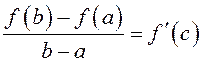

Геометрический смысл теоремы:

y                    B              A                                                                acОbх Рис. 28

АВ – секущая (рис. 28) и  –угловой ее коэффициент.  – угловой коэффициент  касательной.

Так как  , то секущая параллельна касательной. Таким образом, теорема утверждает, что существует касательная, параллельная секущей, проходящей  через точки А и В.

ДОКАЗАТЕЛЬСТВО. Через точки А и В проведем секущую АВ. Ее уравнение 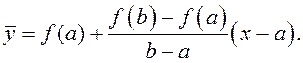 Рассмотрим функцию

,

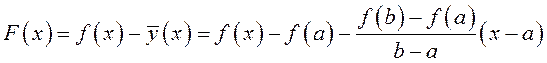 – расстояние между соответствующими точками на графике и на секущей АВ.

1.  непрерывна  как разность непрерывных функций.

2.  дифференцируема   как разность дифференцируемых функций.

3.   

Значит,  удовлетворяет условиям теоремы Ролля, поэтому существует   такая, что 

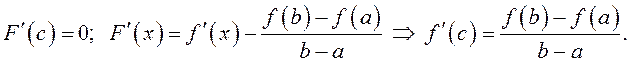
Теорема доказана.

ЗАМЕЧАНИЕ. Формула  называется формулой Лагранжа.

ТЕОРЕМА (Коши). Пусть функции   непрерывны , дифференцируемы   и , тогда существует точка   такая, что  .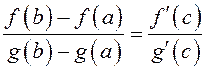

ДОКАЗАТЕЛЬСТВО. Покажем, что . Если бы , то функция   удовлетворяла бы условию теоремы Ролля, поэтому существовала бы точка  такая, что  – противоречие условию. Значит, , и  обе части формулы определены. Рассмотрим вспомогательную функцию  .  

 непрерывна , дифференцируема   и   , то есть   удовлетворяет условиям теоремы Ролля. Тогда  существует  точка , в которой  , но

 

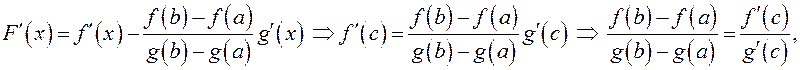
что и требовалось доказать.

Доказанная формула называется формулой Коши.

ПРАВИЛО Лопиталя (теорема Лопиталя-Бернулли). Пусть функции   непрерывны  , дифференцируемы  ,   и  . Кроме того, существует конечный или бесконечный .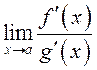

Тогда  существует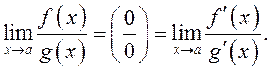 

ДОКАЗАТЕЛЬСТВО. Так как  по условию , то доопределим  в точке , полагая   Тогда  станут непрерывными . Покажем, что    Предположим, что  тогда существует   такая, что  , так как функция  на  удовлетворяет условиям теоремы Ролля. Но по условию   – противоречие. Поэтому   . Функции  удовлетворяют условиям теоремы Коши  на любом отрезке  , который содержится в . Напишем формулу Коши:

,        .

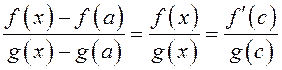Отсюда имеем: , так как если , то . 

Переобозначая переменную в последнем пределе, получим требуемое:

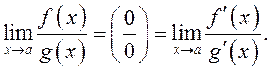
ЗАМЕЧАНИЕ 1. Правило Лопиталя остается справедливым и в том случае, когда   и .  Оно позволяет раскрывать не только неопределенность вида , но и вида  :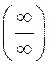

.

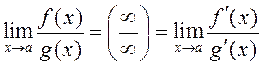ЗАМЕЧАНИЕ 2. Если после применения правила Лопиталя неопределенность не раскрылась, то его следует применить еще раз.

ПРИМЕР.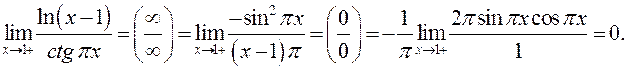

ЗАМЕЧАНИЕ 3. Правило Лопиталя – универсальный способ раскрытия неопределенностей, но существуют пределы, раскрыть которые можно, применив лишь один из изученных ранее частных приемов.

ПРИМЕР. 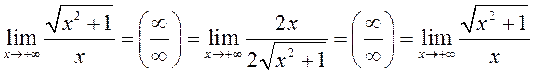 и  так далее.

Но, очевидно, 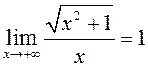, так как степень числителя равна степени знаменателя,  и  предел  равен  отношению  коэффициентов  при  старших  степенях

ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА

ТЕОРЕМА 1 (признак монотонности дифференцируемой функции).

Пусть функция  дифференцируема . Если  то  не убывает, если же   то  не возрастает на .