Математика \ Математика

Введение в математический анализ. Дифференциальное исчисление функции одной переменной: Конспект лекций, страница 4

Заметим, что  Таким образом, всякая монотонная последовательность  ограничена с одной стороны, именно: неубывающая – снизу, невозрастающая – сверху. Значит, для ограниченности неубывающей последовательности необходимо, чтобы она была ограничена сверху, для невозрастающей – снизу.

 ТЕОРЕМА 13. Если неубывающая последовательность ограничена сверху, то она сходится. Если невозрастающая последовательность ограничена снизу, то она также сходится.

Без доказательства.

Из теорем 5,13 следует теорема 14.

ТЕОРЕМА 14. Для того, чтобы монотонная последовательность сходилась, необходимо и достаточно, чтобы она была ограничена.

Рассмотрим последовательность  

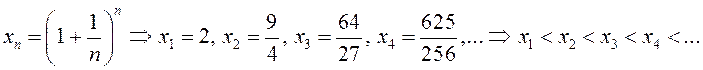
Можно показать, что  возрастает, кроме того, , то есть монотонна и ограничена. Следовательно, по теореме 14  она сходится, то есть  при этом  по теореме 10   Это число обозначают  : оно иррационально, то есть представимо в виде бесконечной десятичной непериодической  дроби,  и  

Таким образом, 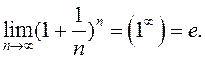    Это равенство называют  вторым замечательным пределом.

Логарифм по основанию  называют натуральным:  

ПРЕДЕЛ  ФУНКЦИИ

Пусть функция  определена на некотором множестве Х действительной оси, которое, быть может, не содержит точку , но содержит точки, бесконечно близкие к   то есть  окрестность этой точки  содержит точки множества Х.

ОПРЕДЕЛЕНИЕ 1 (предел функции в точке  по Гейне). Число  называется пределом функции   в точке   , если для любой

                                 у

                          

b

   

       О             a         x

Рис. 1

последовательности значений ее аргумента  , сходящейся к  и состоящей их чисел, отличных от   соответствующая последовательность значений функций    сходится к    (рис.1). Этот факт обозначается так:

.

ОПРЕДЕЛЕНИЕ 2 (предел функции в точке  по Коши). Число  называется пределом  функции  в точке   , если

,   

Это означает, что всегда найдется такой интервал, содержащий точку  

                                 y                      

b

b

b

О           a     a   a     x

Рис. 2

, всюду внутри которого  отличается от   так мало, как нам захочется.  Так как по определению , то   Если , то, очевидно,  верно неравенство    (рис. 2).

ОПРЕДЕЛЕНИЕ 3 (предел функции на   по Гейне) Число  называется пределом  функции   при , если для любой бесконечно большой  последовательности значений ее аргумента , все члены которой положительны, соответствующая последовательность значений функции   сходится к  (рис. 3). Обозначение:      

                                 

y

                      

b

О                                                          x

Рис. 3

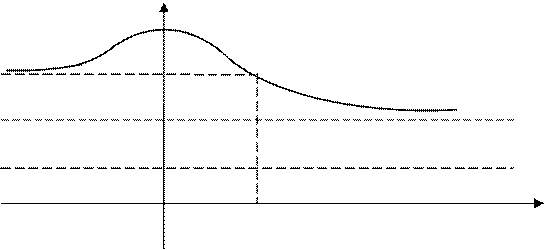ОПРЕДЕЛЕНИЕ 4 (предел функции  на   по Коши).

Число  называется пределом  функции   при , если      (рис. 4).

y

b

b

b

0                                                                          x

Рис. 4

ОПРЕДЕЛЕНИЕ 5 (предел функции на   по Гейне) Число  называется пределом  функции   при , если для любой бесконечно большой  последовательности значений ее аргумента , все члены которой  отрицательны, соответствующая последовательность значений функции   сходится к . Обозначение: 

ОПРЕДЕЛЕНИЕ 6 (предел функции  на   по Коши).  Число  называется пределом  функции   при , если      

Можно доказать, что определения предела по Коши и Гейне эквивалентны.         

ПРИМЕР. Вычислить  .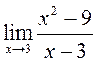

Рассмотрим функцию 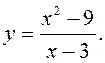   При всех      Выберем произвольную  последовательность   Тогда   независимо от вида  . По определению 1 это означает, что 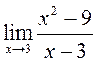   =6.

ТЕОРЕМА (об арифметических операциях над функциями, имеющими предел). Пусть   Тогда существуют пределы в точке  функций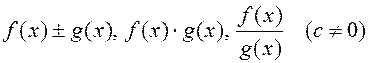   

и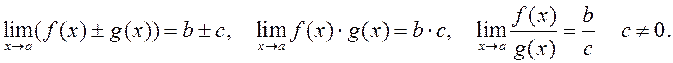        

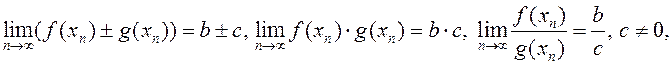ДОКАЗАТЕЛЬСТВО. По условию  По определению 1 выберем произвольную , и   Тогда соответствующие последовательности    и   сходятся к  и  соответственно, то есть   По теоремам 6,7,8,9    что и требовалось доказать.

ОДНОСТОРОННИЕ   ПРЕДЕЛЫ

Скачать файл