Введение в математический анализ. Дифференциальное исчисление функции одной переменной: Конспект лекций, страница 6

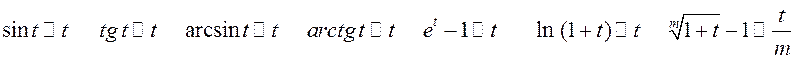
ПРИМЕРЫ. 1) Вычислить 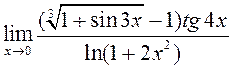.  При     

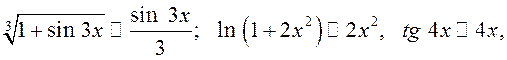
поэтому

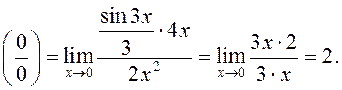
2)   

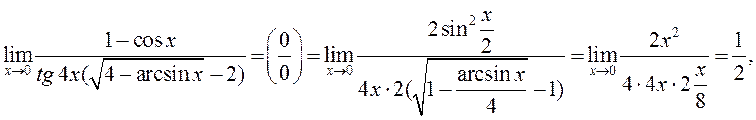
так как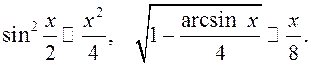    

ЗАМЕЧАНИЕ. Принципом замены б.м. надо пользоваться внимательно. В следующих примерах он не применим.

1) 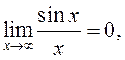  так как числитель ограничен, а знаменатель стремится к бесконечности,

2) 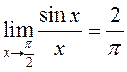  – этот предел неопределенностью не является,

3) 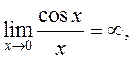  так как .

НЕПРЕРЫВНЫЕ   ФУНКЦИИ

Пусть  входит в область  допустимых значений функции  , причем  не является изолированной точкой.

ОПРЕДЕЛЕНИЕ 1. Функция   называется непрерывной в точке , если

1) существует конечный    существуют конечные и равные односторонние пределы функции в этой точке:

2)

Точки, в которых функция не является непрерывной, называются точками разрыва.

Из определения 1 следует, что   Разность  называется приращением аргумента, а разность   – соответствующим этому приращению приращением функции. Обозначим       

ОПРЕДЕЛЕНИЕ 2. Функция   называется непрерывной в точке , если   где  – приращение функции, соответствующее приращению аргумента  в точке .

y 2 1 -1     О    2       4                 x Рис. 8

ПРИМЕР.  Исследовать функцию   на  непрерывность  в точках    (рис. 8).

1)  в точке  функция непрерывной не является, то есть  – точка разрыва.

2)    также является точкой разрыва.

3)  в точке   функция непрерывна.

ОПРЕДЕЛЕНИЕ. Функция называется непрерывной на интервале, если она непрерывна во всех его точках.

ОПРЕДЕЛЕНИЕ. Функция   называется непрерывной в точке  справа (слева), если  она определена в этой точке и

1) существует конечный 

2)

ОПРЕДЕЛЕНИЕ. Функция называется непрерывной на отрезке , если она непрерывна во всех его внутренних точках и непрерывна справа в точке    и слева в точке  .

График непрерывной функции можно нарисовать без отрыва. Можно показать, что все простейшие элементарные функции

непрерывны на всей области определения.

Непрерывность, например, функции  в точке  означает, что

КЛАССИФИКАЦИЯ  ТОЧЕК  РАЗРЫВА

Непрерывность функции  в точке  означает, что

1) функция в точке  определена,

2)существуют конечные и равные односторонние пределы в этой точке,

3)

Невыполнение хотя бы одного из этих условий говорит о том, что   –

точка разрыва.

ОПРЕДЕЛЕНИЕ. Точка  называется точкой разрыва первого рода, если для функции  существуют конечные пределы   и , причем не все три числа  равны между собой. В частности, если , то точка  называется устранимой точкой разрыва.

ПРИМЕР. 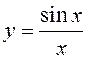      О.Д.З.:                     

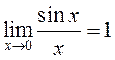, но  не существует. Значит, по определению  – точка разрыва первого рода, причем устранимая.  Такой разрыв можно устранить: для этого нужно доопределить функцию в нуле:

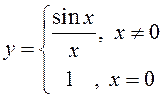 – функция, непрерывная для всех

ПРИМЕР. 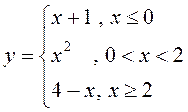   .     Точки  являются точками разрыва первого рода этой функции, причем неустранимого.

Величина    называется скачком функции в точке .

ПРИМЕР. 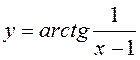   .       О.Д.З. 

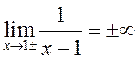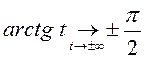Так как    и   ,  то 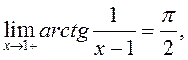 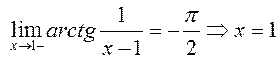  – точка неустранимого разрыва первого рода.

ОПРЕДЕЛЕНИЕ. Точка  называется точкой разрыва второго рода функции   ,   если в этой точке хотя бы один из односторонних пределов бесконечен или не существует.

ПРИМЕР. 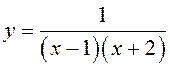    .     О.Д.З.  

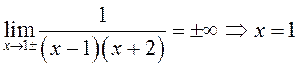 – точка разрыва второго рода,  

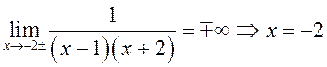 – также точка разрыва второго рода.

ПРИМЕР. 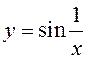  .      О.Д.З. 

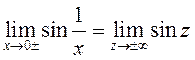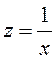, , не существует, значит, по определению  – точка разрыва второго рода.

СВОЙСТВА  НЕПРЕРЫВНЫХ  ФУНКЦИЙ

ТЕОРЕМА. Пусть функции  непрерывны в точке . Тогда 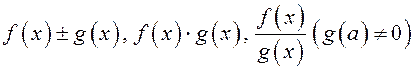 также непрерывны в точке  .

ДОКАЗАТЕЛЬСТВО.

По определению 1 непрерывности функции в точке    Тогда по теореме  об арифметических операциях над функциями, имеющими предел, 

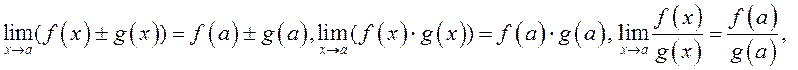
так как  , что и требовалось доказать.

Пусть   определена функция  и  – область ее значений. Кроме того,   определена функция . Тогда говорят, что на множестве  задана сложная функция   (суперпозиция, или композиция функций   и ).

ПРИМЕРЫ. 1)  – композиция функций   и

2) 

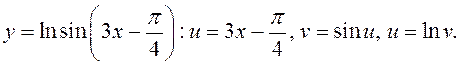
3) 

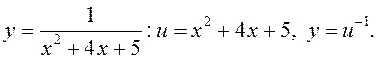
ТЕОРЕМА (о непрерывности сложной функции). Пусть функция  непрерывна в точке  и  Кроме того, функция   непрерывна в точке . Тогда сложная функция  непрерывна в точке .

ДОКАЗАТЕЛЬСТВО. Так как   непрерывна в точке , то по определению 1    Так как   непрерывна в точке  , то  Найдем   Что и требовалось доказать.