ОПРЕДЕЛЕНИЕ.
Пусть заданы две переменные величины ![]() и
и ![]() с областями изменения Х и Y.
Переменная
с областями изменения Х и Y.
Переменная ![]() называется функцией переменной
называется функцией переменной ![]() , если каждому значению
, если каждому значению ![]() из множества Х по некоторому правилу
ставится в соответствие единственное значение
из множества Х по некоторому правилу
ставится в соответствие единственное значение ![]() . Такие
функции называются однозначными.
. Такие
функции называются однозначными.
Чтобы задать функцию, надо
1) задать множество Х,
2)
определить правило установления соответствия между ![]() и
и ![]() .
.
Способы задания функции:
1) аналитический (с помощью формул)
ПРИМЕР. а) ![]() б)
б) ![]()
в) 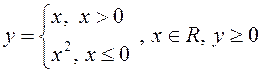 .
.
2) табличный
ПРИМЕРОМ табличного задания функции является расписание.
3) графический.
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
ОПРЕДЕЛЕНИЕ.
Если каждому значению ![]() из
натурального ряда чисел 1,2,3,…,
из
натурального ряда чисел 1,2,3,…,![]() ,…ставится в соответствие
по некоторому правилу действительное число
,…ставится в соответствие
по некоторому правилу действительное число ![]() , то
множество занумерованных действительных чисел
, то
множество занумерованных действительных чисел ![]() называется
числовой последовательностью.
называется
числовой последовательностью.
Таким образом, последовательность – функция натурального аргумента,
![]() называется
общим или
называется
общим или ![]() -м членом последовательности. Зная общий
член
-м членом последовательности. Зная общий
член ![]() , можно найти любой член
последовательности.
, можно найти любой член
последовательности.
ПРИМЕР. ![]()
![]()
ОПРЕДЕЛЕНИЕ. Последовательность ![]() называется
ограниченной сверху (снизу), если
называется
ограниченной сверху (снизу), если ![]()
![]() называется верхней гранью, а
называется верхней гранью, а ![]() нижней гранью последовательности.
нижней гранью последовательности.
ПРИМЕРЫ. а) ![]() =
=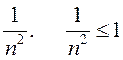 или
или
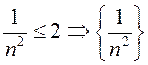 ограничена сверху:
ограничена сверху: ![]()
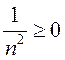 или
или 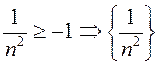 ограничена
снизу:
ограничена
снизу: ![]()
б) ![]() – сверху неограничена и
снизу неограничена.
– сверху неограничена и
снизу неограничена.
в)![]() или
или ![]() ограничена снизу:
ограничена снизу:
![]() Сверху
Сверху ![]() неограничена.
неограничена.
Если последовательность имеет верхнюю или нижнюю грани, то они неединственны.
ОПРЕДЕЛЕНИЕ.
Последовательность ![]() называется ограниченной, если
она ограничена сверху и снизу, то есть
называется ограниченной, если
она ограничена сверху и снизу, то есть ![]()
ПРИМЕР.
![]() ограничена,
так как
ограничена,
так как 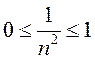 или
или 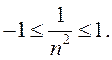
Сформулируем еще одно эквивалентное этому определение ограниченной последовательности, которым, как правило, более удобно пользоваться.
ОПРЕДЕЛЕНИЕ. Последовательность ![]() называется
ограниченной, если
называется
ограниченной, если ![]()
ОПРЕДЕЛЕНИЕ.
![]() называется неограниченной, если для
любого положительного
называется неограниченной, если для
любого положительного ![]() найдется хотя бы один элемент
найдется хотя бы один элемент ![]() такой, что
такой, что ![]()
ОПРЕДЕЛЕНИЕ. ![]() называется бесконечно
большой, если
называется бесконечно
большой, если ![]()
ПРИМЕРЫ. а) ![]() :
2,5,10,17,26,…1001,… – неограниченная и бесконечно большая.
:
2,5,10,17,26,…1001,… – неограниченная и бесконечно большая.
б)
![]() : 0,8,0,32,0,72,… – неограниченная, но не
бесконечно большая.
: 0,8,0,32,0,72,… – неограниченная, но не
бесконечно большая.
Всякая бесконечно большая последовательность неограничена. Обратное утверждение неверно.
ОПРЕДЕЛЕНИЕ.
Последовательность ![]() называется бесконечно малой (б.м.),
если
называется бесконечно малой (б.м.),
если ![]()
ПРИМЕР. 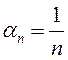 . Если
. Если ![]() , то
, то 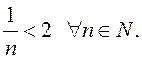
Если ![]() , то
, то 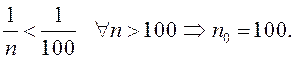
Если ![]() , то
, то 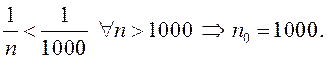
Пусть ![]() произвольно, тогда
произвольно, тогда 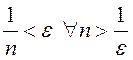 . Таким образом,
. Таким образом, ![]() бесконечно
мала.
бесконечно
мала.
СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Если ![]() ,
, ![]() две последовательности, то
две последовательности, то ![]() называется их суммой,
называется их суммой, ![]() разностью,
разностью, ![]()
![]() произведением, а
произведением, а 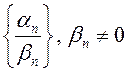 частным.
частным.
ТЕОРЕМА 1. Сумма двух б.м. последовательностей бесконечно мала.
ДОКАЗАТЕЛЬСТВО.
Пусть ![]() б.м. По определению это значит, что
б.м. По определению это значит, что ![]()
Пусть ![]() б.м. По определению
б.м. По определению
![]()
Надо доказать, что ![]()
Зададим
произвольное ![]() . Тогда для
. Тогда для 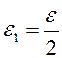
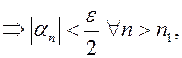 для
для 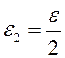
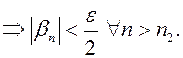 Пусть
Пусть ![]() , тогда
, тогда 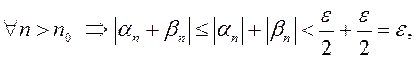 что и
требовалось доказать.
что и
требовалось доказать.
ТЕОРЕМА 2. Разность двух б.м. последовательностей бесконечно мала.
Доказать самостоятельно,
используя неравенство ![]()
ТЕОРЕМА 3. Произведение б.м. последовательности и ограниченной бесконечно мало.
ДОКАЗАТЕЛЬСТВО.
Пусть ![]() б.м., а
б.м., а ![]() ограничена
.Тогда по определению
ограничена
.Тогда по определению ![]() и
и ![]()
Надо доказать, что ![]()
Зададим произвольное ![]() Тогда для
Тогда для 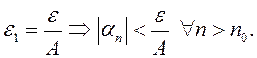 Поэтому
Поэтому
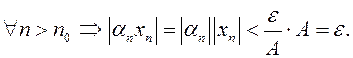 Что и требовалось доказать.
Что и требовалось доказать.
ТЕОРЕМА 4. Всякая бесконечно малая последовательность ограничена.
ДОКАЗАТЕЛЬСТВО.
Пусть ![]() б.м. Тогда по определению
б.м. Тогда по определению
![]()
Положим ![]() Тогда
Тогда ![]()
СЛЕДСТВИЕ. Если ![]() и
и ![]() б.м., то
б.м., то ![]() также
б.м. :
также
б.м. : ![]() по теореме 4 ограничена, тогда по теореме
3
по теореме 4 ограничена, тогда по теореме
3 ![]() б.м.
б.м.
ПРИМЕР. 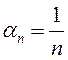 – б.м. Тогда
– б.м. Тогда 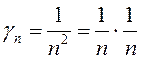 также б.м. И вообще
также б.м. И вообще 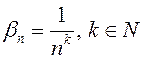 – б.м.
– б.м.
СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
И ИХ СВОЙСТВА
ОПРЕДЕЛЕНИЕ 1.
![]() называется сходящейся, если
называется сходящейся, если ![]() – б.м. Число
– б.м. Число ![]() в этом
случае называется пределом последовательности:
в этом
случае называется пределом последовательности: ![]() . Кроме
того, предел можно обозначать так:
. Кроме
того, предел можно обозначать так: ![]()
ПРИМЕР. ![]() =
=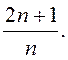 Пусть
Пусть
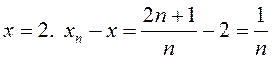 – б.м. Значит, по определению
– б.м. Значит, по определению ![]() сходится к 2:
сходится к 2: 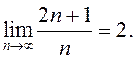
ОПРЕДЕЛЕНИЕ 2.
Число ![]() называется пределом
называется пределом ![]() , если
, если ![]() Последовательность,
имеющая предел, называется сходящейся.
Последовательность,
имеющая предел, называется сходящейся.
Интервал
![]() называется
называется ![]() -окрестностью
точки
-окрестностью
точки ![]() .
.
Из определения 2 следует, что ![]() то
есть
то
есть ![]()
ОПРЕДЕЛЕНИЕ
3. ![]() называется
сходящейся, если
называется
сходящейся, если ![]() такое, что в любой его
такое, что в любой его ![]() -окрестности
-окрестности ![]() содержатся
все члены последовательности, начиная с некоторого.
содержатся
все члены последовательности, начиная с некоторого.
Очевидно, определения 1, 2, 3 сходящейся последовательности эквивалентны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.