Пусть Х – область определения функции, которая, быть
может, не содержит точку ![]() , но для любого
, но для любого ![]() правая полуокрестность точки
правая полуокрестность точки ![]() (интервал
(интервал ![]() ) содержит
точки множества Х.
) содержит
точки множества Х.
ОПРЕДЕЛЕНИЕ 7
(правый предел функции в точке ![]() по Гейне). Число
по Гейне). Число ![]() называется правым пределом функции
называется правым пределом функции ![]() в точке
в точке ![]() , если
для любой последовательности значений ее аргумента
, если
для любой последовательности значений ее аргумента ![]() ,
сходящейся к
,
сходящейся к ![]() и состоящей их чисел, больших
и состоящей их чисел, больших ![]() соответствующая последовательность значений
функций
соответствующая последовательность значений
функций ![]() сходится к
сходится к ![]() . Обозначение:
. Обозначение:
![]()
ОПРЕДЕЛЕНИЕ 8
(правый предел функции в точке ![]() по Коши). Число
по Коши). Число ![]() называется правым пределом функции
называется правым пределом функции ![]() в точке
в точке ![]() , если
, если ![]() ,
, ![]()
Для определения левого предела будем считать, что
любая левая полуокрестность точки ![]() , интервал
, интервал ![]() , содержит точки Х.
, содержит точки Х.
ОПРЕДЕЛЕНИЕ 9
(левый предел функции в точке ![]() по Гейне). Число
по Гейне). Число ![]() называется левым пределом функции
называется левым пределом функции ![]() в точке
в точке ![]() , если
для любой последовательности значений ее аргумента
, если
для любой последовательности значений ее аргумента ![]() ,
сходящейся к
,
сходящейся к ![]() и состоящей их чисел, меньших
и состоящей их чисел, меньших ![]() соответствующая последовательность
значений функций
соответствующая последовательность
значений функций ![]() сходится к
сходится к ![]() . Обозначение:
. Обозначение: ![]()
ОПРЕДЕЛЕНИЕ
10 (левый предел функции в точке ![]() по Коши). Число
по Коши). Число ![]() называется
левым пределом функции
называется
левым пределом функции ![]() в точке
в точке ![]() , если
, если ![]() ,
, ![]()
ПРИМЕР. Найти односторонние пределы (правый и левый) функции
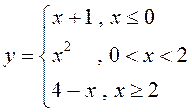
в точках ![]() и
и ![]() .
.
Так как справа от 0 и близко
к нему ![]() то
то ![]() Очевидно,
Очевидно,
![]()

![]() что хорошо видно на графике функции (рис.
5):
что хорошо видно на графике функции (рис.
5):
|
y
1 -1 О 2 4 x Рис. 5 |
Существуют ли |
для того, чтобы функция имела в точке предел , необходимо и достаточно, чтобы в этой точке существовали равные односторонние пределы.
ПРИМЕР. Найти односторонние пределы функции 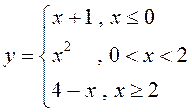 в точке
в точке ![]()
ПРИМЕР. Найти односторонние пределы функции 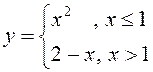 в точке
в точке ![]()
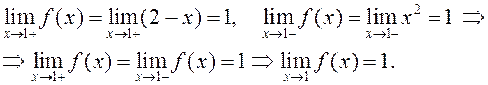
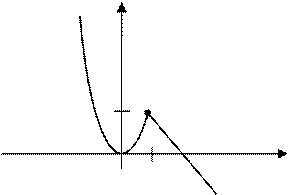 |
|
y
1 О 1 2 x Рис. 6 |
Предел функции в этой точке существует, так как односторонние пределы равны (рис.6). |
СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
ОПРЕДЕЛЕНИЕ. Функция ![]() называется бесконечно
малой (б.м.) в точке
называется бесконечно
малой (б.м.) в точке ![]() если
если ![]()
ПРИМЕРЫ. ![]() – б.м. в точках
– б.м. в точках ![]()
![]() – б.м.
в точках
– б.м.
в точках ![]()
![]() – б.м.
в точке
– б.м.
в точке ![]()
Пусть ![]() и
и ![]() – б.м. в точке
– б.м. в точке ![]() то есть
то есть
![]() Предел отношения б.м. функций
Предел отношения б.м. функций 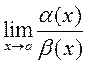 называется неопределенностью вида
называется неопределенностью вида 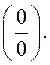
ПРИМЕР. ![]() – б.м. в точке
– б.м. в точке ![]()
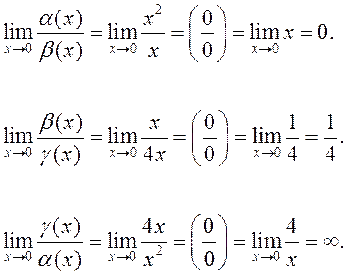
ОПРЕДЕЛЕНИЕ. 1) Б.м. в точке ![]() функция
функция
![]() имеет более высокий порядок малости,
чем
имеет более высокий порядок малости,
чем ![]() , если
, если 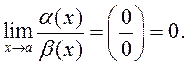
2) Б.м. в точке ![]() функции
функции ![]() и
и ![]() одного порядка малости, если
одного порядка малости, если
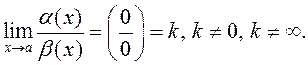
3) Б.м. в точке ![]() функции эквивалентны, если
функции эквивалентны, если
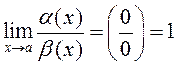 .
.
Эквивалентные б.м.
обозначаются так: ![]()
ПРИМЕР. ![]() имеет более высокий
порядок малости в точке
имеет более высокий
порядок малости в точке ![]() , чем
, чем ![]() и
и ![]()
![]() и
и ![]() одного порядка малости.
одного порядка малости.
ПРИМЕР. Сравнить функции ![]() и
и ![]() , б.м. в точке
, б.м. в точке ![]()
Вычислим предел отношения:
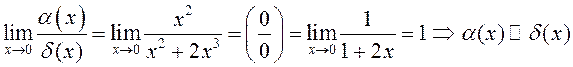
в точке ![]()
ТЕОРЕМА (принцип замены эквивалентных бесконечно малых).
Пусть ![]() б.м. функции в точке
б.м. функции в точке ![]() и
и ![]() Тогда
Тогда
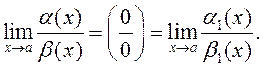
ДОКАЗАТЕЛЬСТВО. Так как ![]() то
то
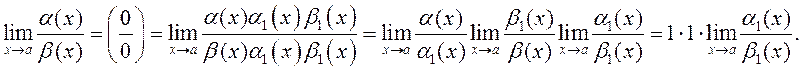
Что и требовалось доказать.
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Докажем,
что 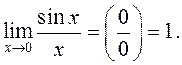 Это равенство называется первым замечательным
пределом.
Это равенство называется первым замечательным
пределом.
Рассмотрим
единичную окружность и угол ![]() радиан. Так как
радиан. Так как ![]() то можно считать, что
то можно считать, что 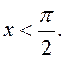
|
C A
0 1 x Рис. 7 |
Очевидно, что
Так как
Разделим неравенство на |
Все выражения здесь положительны, поэтому перейдем к обратным величинам:
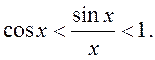 (4)
(4)
Так как функции 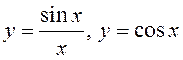 – четные, то есть
– четные, то есть
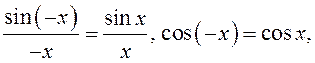
то неравенство (4) верно для
всех 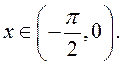 Рассмотрим произвольную
Рассмотрим произвольную ![]() Из (4) имеем:
Из (4) имеем: 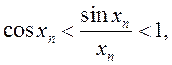 при
этом
при
этом ![]()
Тогда
по принципу двустороннего ограничения (теорема 12) 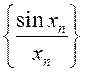 сходится
и
сходится
и 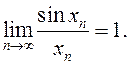 По определению 1 предела функции в точке
по Гейне получаем требуемое:
По определению 1 предела функции в точке
по Гейне получаем требуемое: 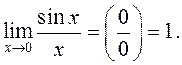
ЗАМЕЧАНИЕ. Доказанное
означает, что в точке ![]() б.м. функции
б.м. функции ![]() и
и ![]() эквивалентны:
эквивалентны:
![]()
ПРИМЕРЫ.
1)Вычислить 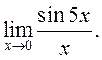
Пусть 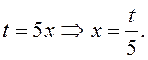 Если
Если
![]() то
то 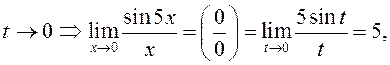
или по-другому: 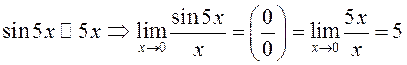 согласно принципу замены б.м.
согласно принципу замены б.м.
2)
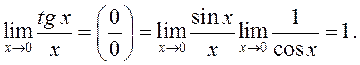
Таким
образом, ![]()
При
рассмотрении неопределенностей вида ![]() можно пользоваться
следующими соотношениями: при
можно пользоваться
следующими соотношениями: при ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.