Введение в математический анализ. Дифференциальное исчисление функции одной переменной: Конспект лекций, страница 14

ДОКАЗАТЕЛЬСТВО. Из определения производной следует, что  – угловой коэффициент касательной к графику в точке  . Заметим (рис. 34), что на участке графика, выпуклом вверх, касательная поворачивается  по часовой стрелке, то есть угол  меняется от острого к тупому, поэтому   убывает. На участке графика, выпуклом вниз, касательная поворачивается против часовой стрелки, то есть  меняется от тупого к острому и  возрастает.

Пусть  убывает по теореме 1, значит,   убывает, и график имеет выпуклость, направленную вверх.

Пусть  возрастает по теореме 1, и график имеет выпуклость, направленную вниз.

Что и требовалось доказать.

ТЕОРЕМА 5 (необходимое условие точки перегиба). Пусть функция  имеет непрерывную вторую производную в некоторой окрестности точки перегиба . Тогда   

ДОКАЗАТЕЛЬСТВО. Пусть   Допустим, . Так как  по условию непрерывна, то по теореме об  устойчивости знака непрерывной в точке функции существует окрестность точки , в пределах которой  , то есть  и справа, и слева от точки . Таким образом, по теореме 4 имеет выпуклость, направленную вниз, и справа, и слева от этой точки. Тогда  по определению точкой перегиба не является. Также приводится к противоречию предположение о том, что . Так как по условию  существует, то, следовательно, , что и требовалось доказать.

ТЕОРЕМА 6 (первое достаточное условие перегиба). Пусть функция  имеет непрерывную вторую производную в некоторой окрестности точки  и . Тогда, если при переходе через    меняет знак, то  – точка перегиба; если  не меняет знак, то  точкой перегиба не является.

ДОКАЗАТЕЛЬСТВО. Доказать самостоятельно, использую теорему 4.

ПРИМЕР. Построить график функции

Ранее были найдены интервалы монотонности этой функции и .

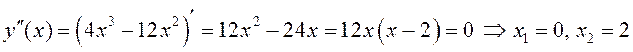 – точки перегиба (рис. 34), .

Строим график с учетом информации о знаках   и   (рис. 35):

АСИМПТОТЫ   ГРАФИКА   ФУНКЦИИ

ОПРЕДЕЛЕНИЕ. Прямая линия называется асимптотой кривой, если расстояние от точки , лежащей на этой кривой, до прямой стремится к  нулю при удалении точки  вдоль одной из ветвей кривой в бесконечность.

ОПРЕДЕЛЕНИЕ. Прямая  является вертикальной асимптотой кривой , если хотя бы один из односторонних пределов в точке   бесконечен.

В этом случае в точке  функция имеет разрыв второго рода.

ПРИМЕР.  Функция   определена при  всех 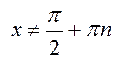, причем 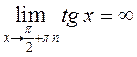, поэтому график этой функции имеет бесконечное множество вертикальных асимптот.

График функции 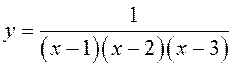 имеет, очевидно, три вертикальные асимптоты: .

ПРИМЕР.  Функция 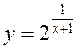 определена при всех  причем 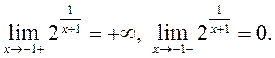  По определению прямая  – вертикальная асимптота графика (справа).

ОПРЕДЕЛЕНИЕ. Прямая  называется наклонной асимптотой графика функции   при , если   представима в виде: 

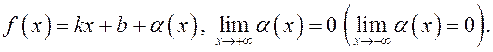
ТЕОРЕМА. Для того, чтобы прямая  была наклонной асимптотой графика функции   при , необходимо и достаточно, чтобы существовали два конечных предела: 

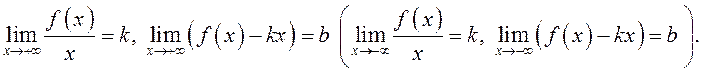
ДОКАЗАТЕЛЬСТВО. Пусть функция  определена при всех достаточно больших положительных значениях .

1. Необходимость:  – асимптота при    существуют конечные пределы

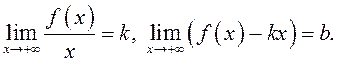
По определению       

Поэтому

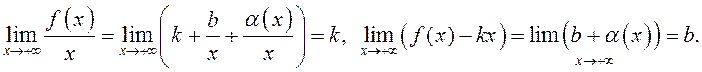
2. Достаточность: существуют конечные 

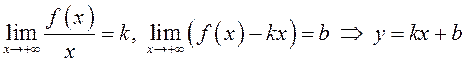
– асимптота при .

По условию                          

Обозначим                          

Тогда   то есть  где  – б.м. при  . По определению  – асимптота , что и требовалось доказать.

Если , доказательство аналогично.