ЗАМЕЧАНИЕ 1.
Всякую бесконечно большую последовательность ![]() будем
трактовать как сходящуюся к бесконечности, именно: если
будем
трактовать как сходящуюся к бесконечности, именно: если ![]() то
то ![]() а
если
а
если ![]()
![]() то
то ![]()
ЗАМЕЧАНИЕ 2. Из определения 3 следует, что отбрасывание любого конечного
числа членов ![]() не изменяет факта ее сходимости и величину
ее предела.
не изменяет факта ее сходимости и величину
ее предела.
ЗАМЕЧЕНИЕ 3.
Из определения 3 следует, что если ![]() сходится, то имеет
единственный предел. Действительно, пусть
сходится, то имеет
единственный предел. Действительно, пусть ![]()
Рассмотрим непересекающиеся окрестности точек ![]() и
и ![]() . Все
члены
. Все
члены ![]() не могут находиться одновременно в них
обеих, следовательно,
не могут находиться одновременно в них
обеих, следовательно, ![]() =
=![]() .
.
Последовательность, не имеющая предела, называется расходящейся.
ПРИМЕР. 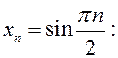 1,0,-1,0,1,0,… Очевидно (определение 3),
что
1,0,-1,0,1,0,… Очевидно (определение 3),
что ![]() расходится, то есть
расходится, то есть 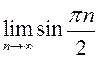 не существует.
не существует.
ПРИМЕР. 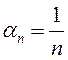 – б.м. Очевидно
(определение 1), что
– б.м. Очевидно
(определение 1), что 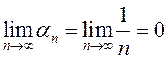 :
: ![]() – б.м.
– б.м.
Таким
образом, если ![]() произвольная б.м., то
произвольная б.м., то ![]()
ТЕОРЕМА
5. Если ![]() сходится,
то
сходится,
то ![]() ограничена.
ограничена.
ДОКАЗАТЕЛЬСТВО.
По определению 1 ![]()
![]() – б.м.
Тогда
– б.м.
Тогда ![]() По теореме 4
По теореме 4 ![]() ограничена,
то есть
ограничена,
то есть ![]() ограничена, что и требовалось доказать.
ограничена, что и требовалось доказать.
ЗАМЕЧАНИЕ. По теореме 5 всякая сходящаяся последовательность ограничена. Обратное утверждение неверно: не всякая ограниченная последовательность сходится.
ПРИМЕР. 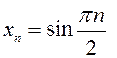 расходится, но
расходится, но 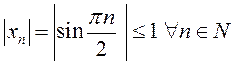 , то есть
, то есть ![]() ограничена.
ограничена.
ТЕОРЕМА
6. Пусть ![]() Тогда
Тогда
![]() сходится и
сходится и ![]()
ДОКАЗАТЕЛЬСТВО.
По определению 1 ![]() где
где ![]() – б.м.
Тогда
– б.м.
Тогда ![]() – б.м. по теореме 1. По определению 1
– б.м. по теореме 1. По определению 1 ![]()
ТЕОРЕМА
7. Пусть ![]() Тогда
Тогда
![]() сходится и
сходится и ![]()
Доказать самостоятельно, используя определение 1 и теорему 2.
ТЕОРЕМА
8. Пусть ![]() Тогда
Тогда
![]() сходится и
сходится и ![]()
ДОКАЗАТЕЛЬСТВО.
По определению 1 ![]() где
где ![]() – б.м.
Тогда
– б.м.
Тогда ![]() – б.м. по теоремам 3,4,1. Что и требовалось
доказать.
– б.м. по теоремам 3,4,1. Что и требовалось
доказать.
ТЕОРЕМА
9. Пусть ![]() Тогда
Тогда
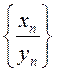 определена, начиная с некоторого номера,
сходится и
определена, начиная с некоторого номера,
сходится и 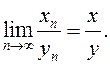
ДОКАЗАТЕЛЬСТВО. Так как ![]() , то выберем
, то выберем ![]() -окрестность точки
-окрестность точки ![]() ,
не содержащую 0. По определению 3 в выбранной
,
не содержащую 0. По определению 3 в выбранной ![]() -окрестности
содержатся все
-окрестности
содержатся все ![]() , начиная с некоторого
, начиная с некоторого ![]() Значит,
Значит,![]() Отбросим
все
Отбросим
все ![]() при
при ![]() (на факт
сходимости и величину предела
(на факт
сходимости и величину предела ![]() это не повлияет ).
это не повлияет ).
По
определению 1 ![]() где
где ![]() – б.м.
– б.м.
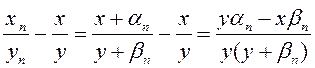 – б.м. по теоремам 2,3,5. Отсюда
– б.м. по теоремам 2,3,5. Отсюда 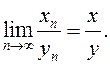
ПРИМЕРЫ. а) Найти
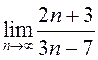 . Так как
. Так как ![]() , то
теорему 9 применить нельзя. Предел, говорят в этом случае, представляет
собой неопределенность вида
, то
теорему 9 применить нельзя. Предел, говорят в этом случае, представляет
собой неопределенность вида 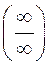 . Чтобы вычислить его,
или раскрыть неопределенность, преобразуем выражение, разделив числитель
и знаменатель на
. Чтобы вычислить его,
или раскрыть неопределенность, преобразуем выражение, разделив числитель
и знаменатель на ![]() :
: 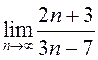 =
=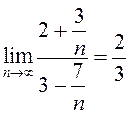 . Ответ получен с помощью теорем 6,7,8,9 и
уже доказанного факта:
. Ответ получен с помощью теорем 6,7,8,9 и
уже доказанного факта: 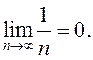
б) 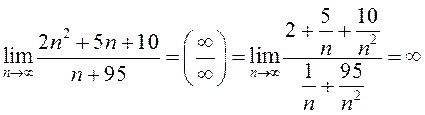
в) 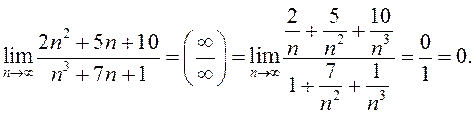
Анализируя рассмотренные пределы и способ их вычисления, можно сформулировать ПРАВИЛО:
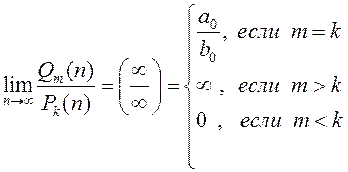 , где
, где ![]() –
степенные функции, зависящие от
–
степенные функции, зависящие от ![]() ,
, ![]() – старшая степень числителя,
– старшая степень числителя, ![]() – старшая степень знаменателя,
– старшая степень знаменателя, ![]() – коэффициент при старшей степени
переменной
– коэффициент при старшей степени
переменной ![]() в числителе,
в числителе, ![]() – коэффициент
при старшей степени переменной
– коэффициент
при старшей степени переменной ![]() в знаменателе.
в знаменателе.
ПРИМЕРЫ. а) 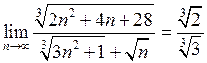 , так как
, так как 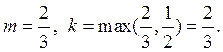
б) 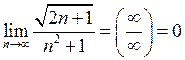 ,
так как
,
так как 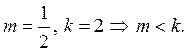
ПРЕДЕЛЬНЫЙ ПЕРЕХОД В НЕРАВЕНСТВАХ
ТЕОРЕМА 10 (о
предельном переходе в неравенстве). Пусть ![]() и,
начиная с некоторого номера,
и,
начиная с некоторого номера, ![]() Тогда
Тогда ![]()
ДОКАЗАТЕЛЬСТВО.
Пусть ![]() Докажем, что тогда
Докажем, что тогда ![]() .
Предположим противное:
.
Предположим противное: ![]() Так как
Так как ![]() сходится, то по определению 2
сходится, то по определению 2 ![]() Пусть
Пусть ![]() Тогда
Тогда
![]() – противоречие, так как по условию
– противоречие, так как по условию ![]() . Таким образом, сделанное предположение неверно
и
. Таким образом, сделанное предположение неверно
и ![]()
Случай ![]() рассматривается
аналогично.
рассматривается
аналогично.
ЗАМЕЧАНИЕ. Предельный переход не сохраняет строгое
неравенство, то есть, если ![]() то
то ![]()
ПРИМЕР. 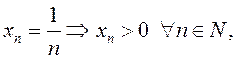 но
но 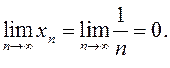
ТЕОРЕМА
11. Пусть ![]() и,
начиная с некоторого номера,
и,
начиная с некоторого номера, ![]() Тогда
Тогда ![]()
Доказать самостоятельно,
используя теоремы 7,10 для ![]() .
.
ТЕОРЕМА
12 (принцип двустороннего
ограничения). Пусть ![]() кроме того, начиная с некоторого
номера,
кроме того, начиная с некоторого
номера, ![]() Тогда
Тогда ![]() сходится
и
сходится
и ![]()
ДОКАЗАТЕЛЬСТВО.
Пусть
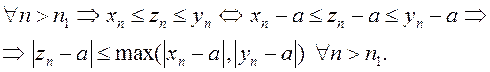 (1)
(1)
По
определению 2 ![]() (2) и
(2) и ![]() (3)
(3)
Зададим
произвольное ![]() Пусть
Пусть ![]() Тогда
неравенства (1),(2),(3) верны
Тогда
неравенства (1),(2),(3) верны ![]() Это означает по
определению 2, что
Это означает по
определению 2, что ![]() сходится и
сходится и ![]() , что и требовалось доказать.
, что и требовалось доказать.
МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
ОПРЕДЕЛЕНИЕ.
![]() называется неубывающей (невозрастающей), если
называется неубывающей (невозрастающей), если
![]() Неубывающая или невозрастающая последовательность
называется монотонной.
Неубывающая или невозрастающая последовательность
называется монотонной.
ОПРЕДЕЛЕНИЕ.
![]() называется возрастающей (убывающей), если
называется возрастающей (убывающей), если ![]() Возрастающая или убывающая последовательность
называется строго монотонной.
Возрастающая или убывающая последовательность
называется строго монотонной.
ПРИМЕРЫ. а) 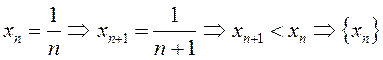 – убывающая.
– убывающая.
б) 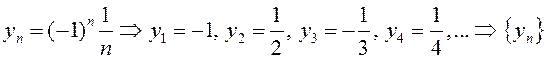 монотонной не является.
монотонной не является.
в)
![]() – возрастающая.
– возрастающая.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.