Оптимальные системы. Основные понятия. Постановка задачи синтеза оптимальных систем. Метод динамического программирования

12. Оптимальные  системы

еред разработчиком системы управления всегда стоит задача формирования в ней наилучших в каком-либо смысле переходных процессов. Чаще всего возникает необходимость обеспечения максимального быстродействия исполнительных механизмов или минимальных затрат энергии на совершение переходных процессов. При этом, естественно, ограничены какие-то внутренние переменные объекта или оговорены дополнительные условия работы. Например, при оптимизации быстродействия системы ограничены, как правило, управляющие воздействия; при оптимизации затрат энергии ограничена длительность переходных процессов. Таким образом, искусство инженера-проектировщика состоит в максимальном удовлетворении заданных требований при известных ресурсных ограничениях.

С развитием техники и теории автоматического управления предъявляемые к системам требования становились все более жесткими, что привело к разработке соответствующих способов проектирования. В 50-х годах XX в. появились математические методы оптимизации переходных процессов: метод динамического программирования Р. Беллмана [1] и принцип максимума Л.С. Понтрягина [10], которые и будут представлены в данном разделе. Ниже рассмотрены основы этих методов и методики проектирования автоматических систем с их применением.

12.1. Основные  понятия

Оптимальной называют такую систему автоматического управления, в которой полностью в каком-либо формальном смысле используются динамические возможности объекта для совершения переходных процессов при заданных ресурсных ограничениях.

Управление, обеспечивающее в системе оптимальные процессы, называется оптимальным и обозначается далее .

Покажем особенности задачи синтеза оптимальной системы на следующем примере.

Пример 12.1

Для объекта, структурная схема которого представлена на рис. 12.1, рассчитать регулятор, обеспечивающий переход из начального положения y(0) в заданное конечное состояние  за минимально возможное время. Ресурс управления объекта ограничен , а k = 1.

Рассмотрим переходные процессы при подаче на вход объекта различных управляющих воздействий (рис. 12.2):

1) если подать управление, численно равное , то переходные процессы в объекте завершатся за время t_п (кривая 1 на рис. 12.2);

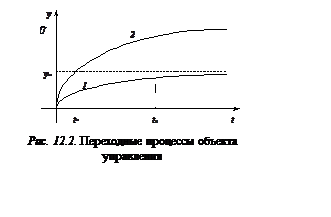2) при подаче на объект максимально возможного управления  на его выходе получим процесс, соответствующий кривой 2, причем в момент времени значение выходной переменной будет равно ;

3) если сначала подать максимально возможное управление  а в момент времени сформировать u = , то процесс перехода в требуемое состояние будет заканчиваться за минимально возможное для объекта время при заданном ограничении на управление.

Реализовать на практике описанный алгоритм управления можно двумя способами:

1.  В виде программного закона управления

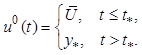
В этом случае оптимальная система будет разомкнутой и, следовательно, не позволит обеспечить требуемые свойства при действии на объект внешних возмущений.

2.  Закон управления в виде обратной связи

Структурная схема замкнутой системы с подобным законом управления представлена на рис. 12.3.

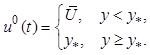
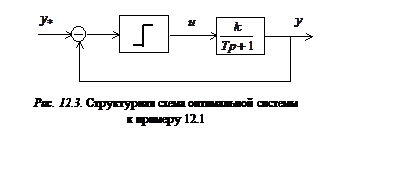Обращаем внимание на то, что полученная релейная система обеспечит оптимизацию переходных процессов при любых параметрах объекта и даже при действии возмущений. Это тот редкий в технике случай, когда алгоритм оптимального управления инвариантен по отношению к возмущениям и нестационарности параметров объекта.

Рассмотренный пример иллюстрирует основные свойства оптимальных систем: объект работает на пределе своих возможностей (полное использование ресурса ), управление имеет релейный характер.

12.2. Постановка  задачи  синтеза  оптимальных  систем

12.2.1. Описание  объекта  управления

Постановка задачи синтеза оптимальных систем предполагает строгую формализацию всех этапов [1 – 3, 5, 10], начиная с описания объекта управления, которое следует представить в переменных состояния. Причем объект должен быть стационарным (параметры не могут изменяться с течением времени), т. е. в общем случае его модель имеет вид

.            (12.1)

Здесь  – вектор состояния объекта;  – вектор нелинейных функций, удовлетворяющих условию существования и единственности решения дифференциального уравнения.

В частном случае объект может быть описан нелинейным стационарным уравнением состояния с аддитивным управлением

,                                  (12.2)

где  – матрица нелинейных функций.

В классе объектов с аддитивным управлением можно выделить подкласс линейных объектов, модель которых имеет вид

.                                      (12.3)

Здесь A и B – матрицы коэффициентов соответствующих размерностей.

12.2.2. Описание  начальных  и  конечных  состояний

На этапе постановки задачи синтеза следует оговорить множество начальных условий объекта и множество конечных состояний, в которые его требуется перевести. Подобный переход удобнее рассматривать в пространстве состояний, причем в зависимости от вида области начальных и конечных состояний можно выделить четыре типа задач синтеза (рис. 12.4.).