Методы синтеза непрерывных адаптивных систем с эталонными моделями. Адаптивная система с настраиваемым коэффициентом усиления. Синтез адаптивных систем градиентным методом. Синтез адаптивных систем по схеме скоростного градиента

Разные суждения у разных,

но верное мало кто знает. (Гесиод)

3. МЕТОДЫ СИНТЕЗА НЕПРЕРЫВНЫХ адаптивных  СИСТЕМ с эталонными моделями

Ограниченность учебного курса и объема учебного пособия не позволяют рассмотреть все существующие методы расчета систем прямого адаптивного управления. Поэтому особенности расчета разобраны на примерах систем с градиентными алгоритмами, ставшими классическими. В этой главе описаны последовательности расчета и некоторые свойства систем, структуры которых определены на основе метода эталонного уравнения, градиентного алгоритма [22, 23], алгоритма скоростного градиента [2, 10, 19, 21, 29], метода функций Ляпунова [2, 16, 19]. В начале главы дано описание адаптивной системы с настраиваемым коэффициентом усиления, идея синтеза которой появилась одной из первых в практике адаптивного управления. Пример этой системы напоминает о свойствах обратной связи, рассмотренных в курсе «Теория автоматического управления».

3.1  Адаптивная система с настраиваемым коэффициентом усиления

Известно, что отрицательная обратная связь  позволяет уменьшить влияние изменений параметров устройств, образующих прямой канал системы, т.е. объекта управления, исполнительного механизма, преобразователя и т.д. [31]. Рассмотрим простую систему регулирования с единичной обратной связью (рис. 3.1).

Рис. 3.1

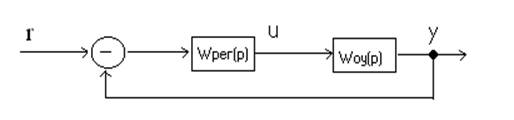
На рис. 3.1 передаточные функции объекта управления и регулятора обозначены W_оу(р), W_рег(р) соответственно. Определим передаточную функцию замкнутой системы

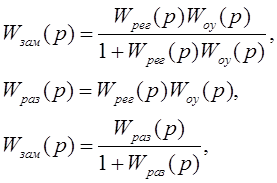
Чувствительность свойств замкнутой системы от свойств разомкнутой [11, 31] определяется выражением

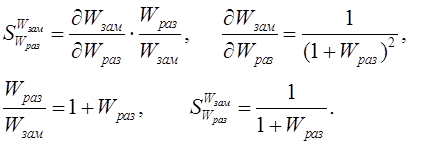
Таким образом, чувствительность обратно пропорциональна множителю (1+W_раз). Если в некотором диапазоне частот  хотя бы за счёт увеличения коэффициента передачи регулятора, то чувствительность замкнутой системы к изменению параметров будет уменьшена. Однако увеличение коэффициента передачи ограничено условиями устойчивости и рабочими характеристиками. Эти ограничения можно преодолеть в ряде случаев, если ввести в систему цепь адаптации. Адаптивная система с настраиваемым коэффициентом усиления была использована в автопилоте корпорации Миннеаполис – Ханивелл (Minneapolis- Honneywell; Prince L.T., Hendrick R.C., Lindahl J.H. Honneywell’s Flight Control System,  Symposium on Adaptive Control, 1960). Схема системы приведена на  рис. 3.2.

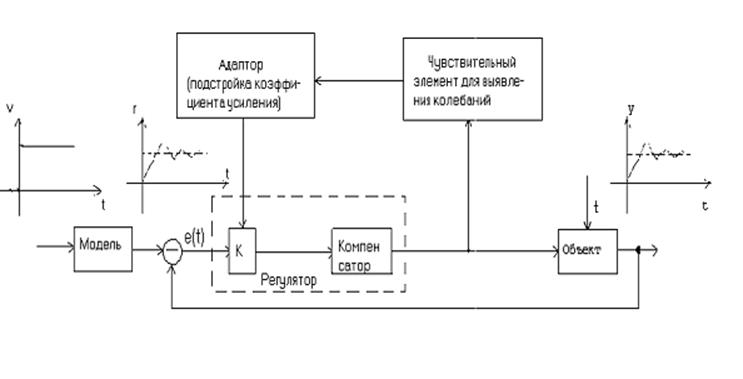
Рис. 3.2

Коэффициент передачи и, как следствие, ширина зоны пропускания поддерживаются на требуемом уровне с помощью цепи адаптации. С увеличением коэффициента передачи замкнутая система приближается к границе устойчивости. Так как в рабочей полосе частот |W_зам(jω)|»1, то выходная переменная системы достаточно близка к эталонному входному сигналу (r(t)).  Эталонный входной сигнал можно получить с помощью простой модели (например, с помощью электрической цепи), а чтобы адаптация давала приемлемую точность, рекомендуется установить полосу пропускания модели на уровне 1/3 ширины пропускания замкнутой системы. При этих условиях адаптивная система практически нечувствительна к изменениям параметров объекта управления. Изменение коэффициента передачи зависит от колебательности процессов в системе. На наличие колебаний проверяется либо управляющий сигнал, либо сигнал ошибки.

Некоторыми недостатками системы можно считать следующее

1)  модель объекта управления должна быть известна для того, чтобы удерживать полюсы замкнутой системы достаточно далеко от мнимой оси;

2)  в цепи управления постоянно присутствуют небольшие колебания. На практике амплитуда колебаний может поддерживаться на уровне ниже порога чувствительности пилота, и поэтому она может не влиять на полет.

3.2 Синтез адаптивных систем  градиентным методом

Градиентный алгоритм относится к базовым алгоритмам адаптации [19, 22, 23]. Вектор градиента всегда направлен в сторону максимального локального роста функции. Пусть k - аргумент функции Q,  тогда чтобы реализовать  последовательный спуск в локальный минимум функции Q, следует направить вектор скорости параметров () в сторону антиградиента ,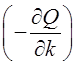

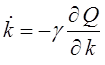 .                                                     (3.1)

3.2.1 Расчет адаптивного регулятора для объекта первого порядка

Общий подход к последовательности синтеза системы градиентным методом рассмотрим на примере скалярного объекта первого порядка:

.

Эталонной модели можно поставить в соответствие уравнение вида

, где  . Обозначим рассогласование между  и  через e : . Цель функционирования системы можно задать асимптотическим выражением:  при . Используя известные методы синтеза, например, метод эталонного уравнения, закон управления получим в виде:

, где  – настраиваемый коэффициент регулятора. После подстановки закона управления в уравнение объекта управления получим уравнение обобщенного настраиваемого объекта

.

Достижение поставленной цели управления можно анализировать с помощью функции цели , если   при  , то , что и требуется по условию задачи. В соответствии с градиентным методом алгоритм адаптации запишем в виде