Методы синтеза непрерывных адаптивных систем с эталонными моделями. Адаптивная система с настраиваемым коэффициентом усиления. Синтез адаптивных систем градиентным методом. Синтез адаптивных систем по схеме скоростного градиента, страница 5

Реальный закон управления имеет вид

                                    (3.32)

где k^x (t), k^r (t) – матрицы настраиваемых коэффициентов регулятора, 

Для определения вида алгоритма адаптации требуется вычислить производную целевого функционала в силу уравнений системы, т.е.

                     (3.33)

После подстановки (3.32) в (3.33) имеем

  (3.34)

Определим скоростные градиенты

Для алгоритмов настройки коэффициентов выбираем АСГ в дифференциальной форме

                    (3.35)

где Г = gI,  g > 0 .

Система (3.25), (3.26), (3.32), (3.35) относится к системам с параметрической адаптацией. На основе АСГ можно синтезировать также системы с сигнальной и сигнально-параметрической адаптацией. Структурная схема системы изображена на рис. 3.10, где использованы обозначения:    ,  ,  x1 = x_м , k1 = k^r ,  k = k^x ,  A1 = B^TH.

Системы с алгоритмом адаптации (3.35) сохраняют работоспособность при изменении координатных и параметрических возмущений в широких пределах.  Качество процессов ухудшается, если скорость изменения параметрических возмущений высокая. С целью повышения быстродействия в контурах параметрической настройки коэффициентов регулятора можно применять пропорционально- интегральные алгоритмы адаптации в конечно- дифференциальной форме

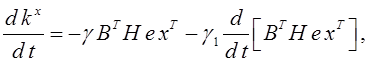
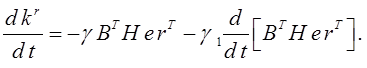                       (3.36)

В рассмотренной последовательности синтеза адаптивного регулятора можно выделить следующие этапы:

1.  Задание функции цели,

2.  Определение уравнения контура модель-объект при x = x_м ,

3.  Определение «идеального» закона управления,

4.  Определение условия существования идеальных коэффициентов регулятора (рангового условия),

5.  Нахождение реального закона управления, введение настраиваемых коэффициентов,

6.  Определение градиента целевой функции,

7.  Определение алгоритма адаптации в дифференциальной форме,

8.  Определение алгоритма адаптации в конечно-дифференциальной форме.

Замечание: В алгоритмы (3.35), (3.36) входят элементы матрицы коэффициентов объекта В, которые, в общем случае, неизвестны. Если эталонная модель достаточно точно описывает объект в номинальном режиме работы, то в алгоритм адаптации вместо В можно использовать В_м.

Рис. 3.10

Пример 3.2.Проведем синтез адаптивного регулятора для объекта, рассмотренного в примере 3.1. Уравнение эталонной модели (3.20) запишем в виде

                                        (3.37)

здесь y_м- выходная переменная b_ом = a_ом = 2,  т.е. эталонная динамика системы формируется динамическим звеном (3.37). Если рассогласование по выходным переменным задать выражением

                                                 (3.38)

то функцию качества (3.28) можно записать следующим образом

                                                 (3.39)

Уравнение регулятора (3.32) с учетом модели объекта (3.37) имеет  вид

                                           (3.40)

где k^y, k^r - настраиваемые коэффициенты. Тогда полная производная функции (3.39) есть

                 (3.41)

а частные производные функции (3.41) по настраиваемым коэффициентам

.

Алгоритм настройки коэффициентов регулятора с учетом (3.40) и (3.23) получим в виде

   .                         (3.42)

Структурная схема системы (3.19), (3.37), (3.40), (3.42) приведена на рис. 3.11 (использованы  обозначения   ).

Рис. 3.11

Процессы в системе с постоянными параметрическими возмущениями и  коэффициентом передачи адаптора =50 приведены на рис. 3.12, а с переменными параметрическими возмущениями () и =30  - на рис. 3.13.

3.4 Синтез адаптивных систем методом функций Ляпунова

Второй метод Ляпунова был разработан для исследования устойчивости движения нелинейных систем, которые описываются обыкновенными дифференциальными уравнениями [4, 18].

Александр Михайлович Ляпунов (1857 – 1918 гг.)