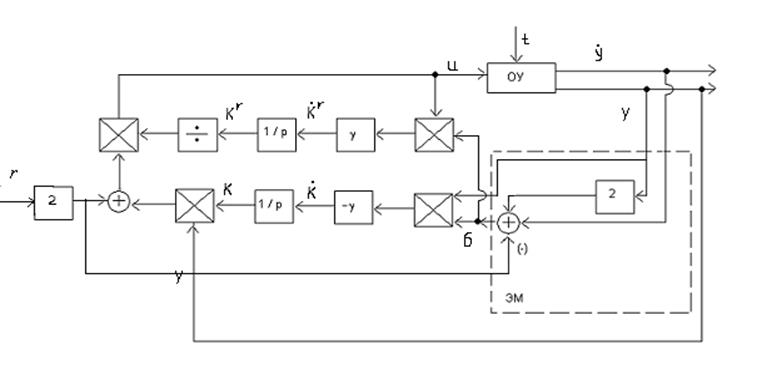
Другие предметы \ Системы автоматического управления

Методы синтеза непрерывных адаптивных систем с эталонными моделями. Адаптивная система с настраиваемым коэффициентом усиления. Синтез адаптивных систем градиентным методом. Синтез адаптивных систем по схеме скоростного градиента, страница 4

Рис. 3.6

По сравнению с предыдущим случаем (рис. 3.3, 3.4) в данной системе для достижения удовлетворительного качества выходных процессов требуется меньшее значение коэффициента передачи адаптора.

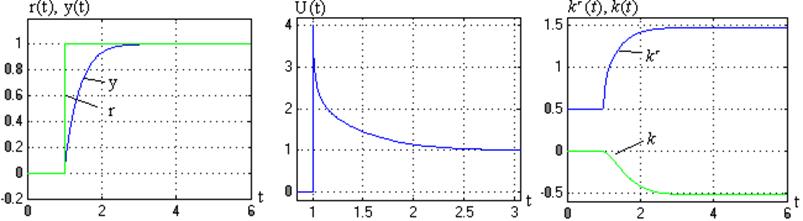
Рис. 3.7

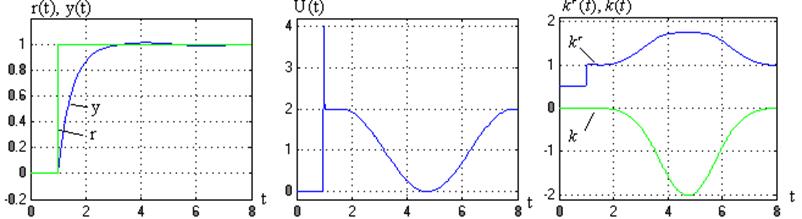
Рис. 3.8

3.3 Синтез адаптивных систем по схеме скоростного градиента

3.3.1 Общая характеристика схемы скоростного градиента

Идея схемы скоростного градиента принадлежит Красовскому А.А., который для задачи идентификации с адаптивной моделью предложил общий вид алгоритма адаптации, оптимального по критерию обобщенной работы. Алгоритм скоростного градиента (АСГ) нашел дальнейшее развитие в работах Фрадкова А.Л., Деревицкого Д.П., Андриевского Б.Р. и других специалистов в области теории управления. Суть метода скоростного градиента заключается в следующем: настройка параметров осуществляется в направлении, противоположном скорости изменения целевого функционала вдоль траектории обобщенного настраиваемого объекта.

Пусть ОНО описывается уравнением , где f (x,q, t) – вектор-функция, q - вектор-функция настраиваемых коэффициентов. Алгоритмом скоростного градиента принято называть правило изменения настраиваемых коэффициентов (q ), задаваемое уравнением вида

(3.22)

где 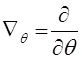- дифференциальный оператор, Г = Г ^Т > 0 – квадратная матрица коэффициентов передачи,

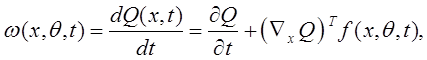
здесь Q(.) – целевая функция; y– вектор-функция, удовлетворяющая условию псевдоградиентности:

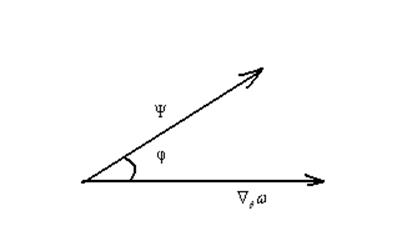
(см. Приложение 1). Это условие эквивалентно требованию, по которому угол j между векторами y и w должен находиться в пределах от - 90⁰ до + 90⁰ (рис. 3.9). Условие псевдоградиентности выполняется, если

или

(аргументы вектор-функции опущены для упрощения записи выражений),

Г_i^T = Г_i > 0 – квадратная матрица коэффициентов (i = 1, 2), Г₂ – диагональная матрица, sgn (.) – вектор, состоящий из знаков компонент вектора Ñ_qw.

- 90⁰ ≤ j ≤ 90⁰

Рис. 3.9

АСГ вида (3.22) называют алгоритмом в конечно-дифференциальной форме. Частными случаями (3.22) являются алгоритмы в дифференциальной форме (при y = 0)

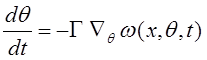(3.23)

и в конечной форме (для Г = 0)

(3.24)

где t - шаг дискретизации.

3.3.2 АСГ в системах с явной реализацией эталонной модели

Рассмотрим пример синтеза системы с параметрической адаптацией. Сформулируем задачу синтеза для объекта управления, который задан моделью в пространстве состояний

(3.25)

где xÎRⁿ , uÎR^m – векторы состояния и входа ОУ, , – матрицы неизвестных коэффициентов соответствующих размерностей, известно лишь, что значения коэффициентов ограничены по модулю, т.е.

для всех i, j, r, p.

Уравнение эталонной модели выбрано в форме

(3.26)

где rÎR^m– задающее воздействие, А_м – гурвицева матрица. Цель управления сформулирована относительно координатного рассогласования

(3.27)

где e(t)=x(t)–x_м(t). Предполагаем, для объекта (3.25) выполняются условия управляемости и наблюдаемости координат состояния. Пусть целевая функция имеет вид квадратичной формы

(3.28)

Поставленная цель управления выполняется, если Q®0 при t®¥.

Синтез адаптивного регулятора начнем с определения уравнения основного контура. Допустим, что , тогда справедливо равенство . Вычтем (3.26) из уравнения (3.25):