Методы синтеза непрерывных адаптивных систем с эталонными моделями. Адаптивная система с настраиваемым коэффициентом усиления. Синтез адаптивных систем градиентным методом. Синтез адаптивных систем по схеме скоростного градиента, страница 7

  .                                        (3.52)

Обозначим расширенную матрицу отклонений настраиваемых коэффициентов от их «идеальных» значений через ,

, а вектор сенсоров - s, элементы этого вектора измеряются или вычисляются на основе измерений,

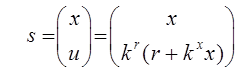,     dim s = p x 1,   p = n + m.

Уравнение (3.52) с учетом введенных обозначений примет вид

.

Полученное уравнение является уравнением системы в отклонениях.

Исследование системы проведем с помощью функции, зависящей  от координатных и параметрических рассогласований,

,                 (3.53)

где tr (.) – след матрицы, который определяется как  сумма элементов главной диагонали (см. Приложение 1). В силу уравнения (3.52) определим производную по времени функции V :

.

Вторая составляющая уравнения обращается в нуль, если

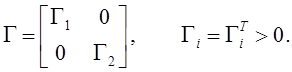            (3.54)

Уравнение (3.54) описывает алгоритм адаптации в отклонениях. Производная исследуемой функции принимает вид

отрицательная определенность следует из свойства гурвицевости матрицы коэффициентов эталонной модели  и положительности матрицы Н, удовлетворяющей уравнению Ляпунова:

Полагая медленное изменение коэффициентов () и учитывая ранее введенные обозначения, получим вид алгоритмов адаптации:

,                                          (3.55)

    

Структурная схема адаптивной системы (3.25), (3.26), (3.46), (3.55) изображена на рис. 3.14 . Приняты следующие обозначения элементов схемы:

.

Условия, при которых решена поставленная задача, являются условиями идентифицируемости  при  и, одновременно, асимптотической устойчивости в целом

Синтез  адаптивной системы на основе второго метода Ляпунова состоит из следующих этапов:

1.  Определение порядка и параметров эталонной модели;

2.  Определение «идеального»  закона управления;

3.  Введение матриц идеальных коэффициентов регулятора;

4.  Проверка условий согласованности модели и объекта управления;

5.  Формирование реального закона управления;

6.  Определение уравнения обобщенного настраиваемого объекта в отклонениях;

7.  Проверка устойчивости системы вторым методом Ляпунова;

8.  Определение условия отрицательной определенности производной выбранной функции относительно матрицы параметрических рассогласований;

9.  Определение вида алгоритма адаптации.

Пример 3.3.  Используя приведенную выше последовательность действий, выполним расчёт  регулятора для одноканального объекта первого порядка

 

где      Объект управления первого порядка, поэтому желаемую динамику системы зададим уравнением

   >0 , причем  так как в статике должно выполнятся равенство  В процессе синтеза основного контура получим уравнение системы в отклонениях

 

  

                           (3.56)

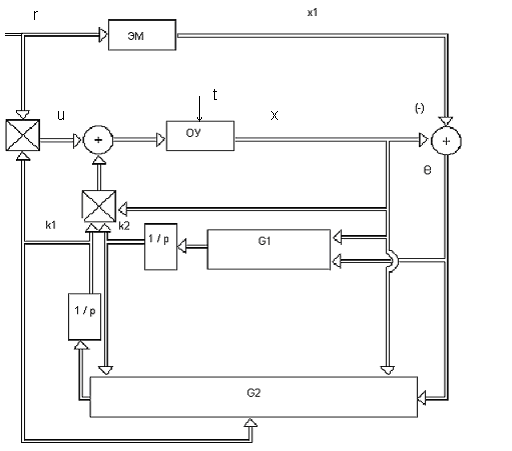
Рис. 3.14

Из условия разрешимости задачи синтеза основного контура определим “идеальный” закон управления:

        

Идеальные значения коэффициентов связаны с параметрами объекта и системы следующим образом

                        (3.57)

В реальный закон управления введём коэффициенты  :

                                             (3.58)

и модель обобщённого настраиваемого объекта запишем в виде

Используя обозначения параметрических рассогласований

      

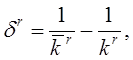
и подставив (3.58)  в  (3.56) , запишем уравнение  в отклонениях

Из (3.57) выражаем   bи :

    

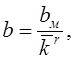
тогда уравнение в отклонениях можно записать в виде

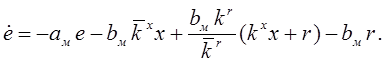
К правой части последнего уравнения добавим и отнимем , после чего получим 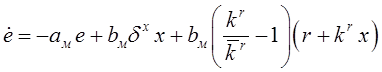   или, учитывая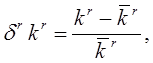

                        (3.59)

Матрица отклонений и вектор сенсоров имеют вид

                          (3.60)

Уравнение (3.59) с учётом (3.60) преобразуем к виду       

Анализ сходимости процессов в системе и одновременно определение алгоритма настройки коэффициентов выполним с помощью функции V:

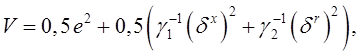
где H=I ,  .

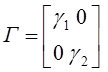Определим полную производную выбранной функции

Алгоритм адаптации найдём из условия  < 0 , для этого потребуем выполнения равенства