Для определения целевой функции введем новое рассогласование (s) , которое возникает в результате замены yм на yв уравнении эталонной модели (3.5),
(3.13)
Если вычесть из (3.13) уравнение (3.5), то получим уравнение, описывающее связь между рассогласованиями e и s :
(3.14)
Из (3.14) следует, что если s® 0 при t®¥, то в силу устойчивости 
e® 0 при t®¥ . Следовательно, будет выполнена
поставленная цель. Это позволяет задать целевую функцию в виде
(3.15)
Выполним преобразования уравнения (3.13). Просуммируем уравнения объекта (3.8) и регулятора (3.12):
, приведем подобные и учтем (13):
(3.16)
Из коэффициентов полиномов 
образуем векторы 
и
соответственно. Введем обозначения для
вектора неизвестных параметров
вектора настраиваемых параметров
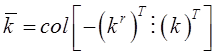
и вектора координатных переменных
Уравнение для рассогласования (3.16) примет вид
.
(3.17)
Алгоритм настройки коэффициентов согласно (3.1), (3.15), (3.17) имеет вид
или
(3.18)
Структурная схема адаптивной системы
(3.2), (3.12), (3.18) изображена на рис.3.5, где приняты следующие обозначения 
, 
.
Для определения вида алгоритмов управления и настройки коэффициентов выполнена следующая последовательность преобразований уравнений системы:
1. Введена ошибка системы по выходным переменным (e).
2. Введена обобщенная ошибка (σ).
3. Выбрана функция цели (Q).
4. Введен оператор параметрического рассогласования (Δ(p)).
5. Определен вид «идеального» закона управления.
6. Выполнен переход к реальному закону управления.
7. Определена связь между обобщенной ошибкой и ошибкой по выходной переменной. Доказано свойство e → 0 при t → ∞, если σ→ 0.
8. Определено уравнений обобщенного настраиваемого объекта в отклонениях.
9. На основе градиентной процедуры определен вид алгоритма адаптации.
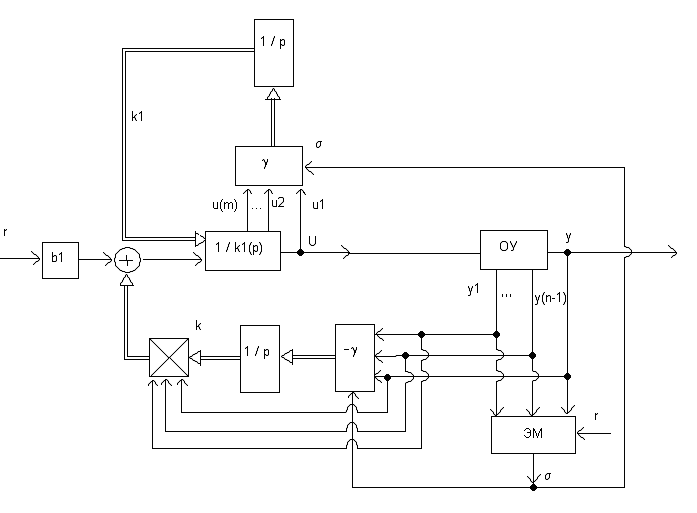
Рис. 3.5
Замечание: Основная трудность при синтезе алгоритмов адаптации градиентным методом заключается в определении функции чувствительности, так как закон изменения параметров объекта не известен. В случае, когда система и модель операторно тождественны, то функцию чувствительности можно получить, используя оператор (передаточную функцию) ЭМ. Но при этом повышаются требования, предъявляемые к ЭМ, и, тем самым, исключается возможность использовать в качестве ЭМ динамическое звено меньшего порядка по сравнению с реальной системой. Другой способ преодоления трудности в определении функции чувствительности состоит в использовании вспомогательного оператора.
Пример 3.1. Выполним расчет адаптивной системы для наиболее простого случая. С этой целью рассмотрим объект управления первого порядка
, (3.19)
здесь a0 (t), b0 (t) – неизвестные медленноменяющиеся параметры. Процессы в системе должны удовлетворять следующим показателям качества: s% »0%, tn £ 3c, а в установившемся режиме должно выполняться предельное неравенство
В соответствии с заданными показателями качества определим дифференциальное уравнение эталонной модели
(3.20)
Согласно (3.12) и (3.18) уравнения регулятора и адаптора имеют вид
(3.21)
Структурная схема системы с градиентным алгоритмом адаптации имеет вид, изображенный на рис. 3.6.
Процессы в системе со
стационарным объектом управления и 
=2 приведены на рис.
3.7. На рис. 3.8 показаны выходные процессы системы, регулятора и адаптора при
нестационарном объекте управления (
) и коэффициенте
передачи =20. Достижение поставленной цели
управления определяем по виду выходной переменной, сравнивая показатели
качества с заданными значениями. Так как в контуре настройки 
присутствует блок, выполняющий функцию
деления, то начальные условия на интеграторе должны быть отличны от нуля.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.