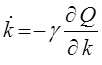Методы синтеза непрерывных адаптивных систем с эталонными моделями. Адаптивная система с настраиваемым коэффициентом усиления. Синтез адаптивных систем градиентным методом. Синтез адаптивных систем по схеме скоростного градиента, страница 2

   или 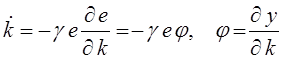   , где φ – функция чувствительности. Данный алгоритм обеспечивает изменение настраиваемого коэффициента в каждый текущий момент времени, направленное на минимизацию функции цели. Принимая во внимание, что , функция чувствительности может быть определена через передаточную функцию. Основная трудность при синтезе таких алгоритмов заключается в определении φ, так как закон изменения параметров объекта не известен. В случае, когда система и модель операторно тождественны, то φ  можно получить, используя оператор (передаточную функцию) эталонной модели. Но при этом исключается возможность выбора ЭМ в виде динамического звена меньшего порядка по сравнению с объектом управления. В частном случае уравнение адаптора может иметь вид:

.

Объект управления, эталонная модель, регулятор и адаптор образуют адаптивную систему. Процессы, наблюдаемые в замкнутой системе при отработке постоянного входного воздействия единичной амплитуды и , приведены на рис. 3.3 и 3.4. Выходной сигнал достигает заданного эталонного значения после окончания переходного процесса. Точность в установившемся процессе выше в системе со стационарным объектом (рис. 3.3).

Рис. 3.3.

Моделирование выполнено при коэффициенте передачи равном -=60  и начальном условии в адапторе -  k(0)=1. Для парирования переменного параметрического возмущения (рис. 3.4), которое задавалось функцией вида , потребовалось большее значение коэффициента передачи адаптора:  =80,  начальные условия в контуре настройки те же, что и в предыдущем случае:   k(0)=1. В зависимости от свойств возмущения на выходах регулятора и адаптора в установившемся режиме наблюдаются либо постоянные значения, либо колебания соответствующих переменных (рис. 3.3, 3.4).

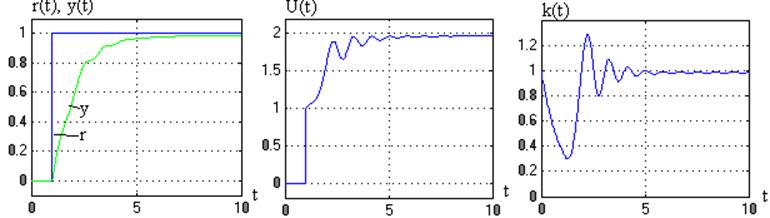
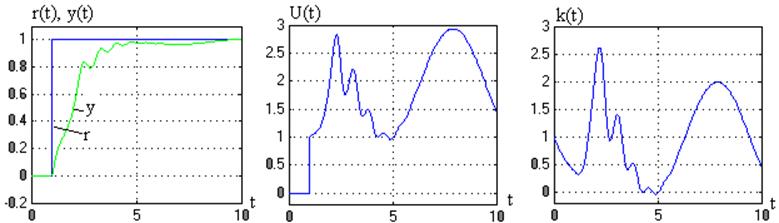
Рис.3.4.

3.2.2 Расчет адаптивного регулятора для объекта n-ого порядка

Проведем синтез адаптивной системы для одноканального линейного объекта управления

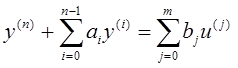                                           (3.2)

где  – управляющая и выходная переменные соответственно, . Параметры объекта  точно не определены, но заданы (n + m + 1) – мерной областью возможных значений W_ab. Операторная запись уравнения (3.2) имеет вид

                                                   (3.3)

где

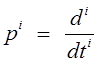– оператор i- кратного дифференцирования. Считаем, что в выражении (3.3) полином при управляющем воздействии () является устойчивым.

Цель управления зададим предельным соотношением

                                                 (3.4)

где – эталонная траектория движения, которая удовлетворяет уравнению эталонной модели

                                                                                (3.5)

здесь 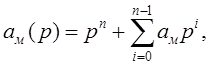   – эталонное входное воздействие на систему. Полином  является устойчивым, т.е. корни уравнения = 0 имеют отрицательную действительную часть.

Для определения структуры “идеального” закона управления выполним преобразования уравнений (3.2) и (3.5). Вычтем из обеих частей уравнения (3.3) выражение ():

.                                             (3.6)

Полагая , запишем уравнение (3.5)

                                                     (3.7)

Прибавим к обеим частям уравнения (3.6) выражение () :

                                  (3.8)

где 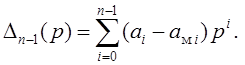 Далее вычтем из (3.8) уравнение (3.5):

                                    (3.9)

где . Пусть “идеальный” закон управления имеет вид

                                         (3.10)

тогда

                                                    (3.11)

Так как полином  является устойчивым по условию, то при , т.е. закон управления (3.10) позволяет обеспечить выполнение цели управления (3.4). Учитывая, что  и  не известны, реальный закон управления запишем в виде

                                            (3.12)

с операторами 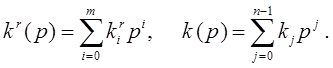 Если в процессе настройки коэффициентов будет выполнено  при t®¥ ,  то   e® 0,  что соответствует достижению поставленной цели управления.