|
Р |
азвитие технологических процессов в промышленности часто приводит к необходимости текущей оптимизации (настройки на экстремум) отдельных агрегатов. В случае, когда требуется на экстремальном уровне поддерживать некоторый показатель качества работы динамической системы, зависящий от параметров объекта и действующих на него возмущений, необходимо создавать специальные автоматические системы, которые называют экстремальными или системами автоматического поиска экстремума.
Такая задача возникает, например, при поддержании скорости полета самолета, соответствующей минимуму расхода горючего на единицу длины пути. Примером системы автоматического поиска экстремума является система поддержания максимальной скорости проходки скважины турбобуром при меняющихся свойствах грунта [10, 11].
Содержанием этого раздела является решение задачи поиска экстремума методами теории автоматического управления. При этом большое внимание уделяется вопросу оценки градиента выходной характеристики системы.
11.1. Основные понятия и определения
Системой поиска экстремумабудем называть такую систему автоматического управления, которая в процессе работы обеспечивает достижение минимума или максимума некоторого показателя качества при недостаточной априорной информации о характере его изменений. При этом ни количество экстремумов, ни их положение, ни аналитическое выражение функции качества в общем случае могут быть неизвестны.
Под действием различных возмущений экстремальная характеристика объекта Y(y) может смещаться или, как принято говорить, дрейфовать с искажением или без искажения формы. При этом можно выделить следующие виды дрейфа:
- вертикальный дрейф – положение экстремума изменяется по вертикали (рис. 11.1,а);
- горизонтальный дрейф – экстремум смещается по горизонтали;
- смешанный дрейф – экстремум изменяет положение и по вертикали, и по горизонтали (рис. 11.1,б).
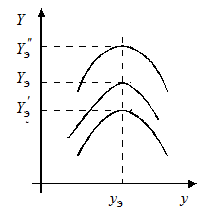
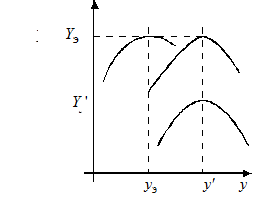
a б
Рис. 11.1. Иллюстрация дрейфа экстремальной характеристики:
a – по вертикали; б – по горизонтали и по вертикали
В первом случае достаточно каким-либо образом (аналитически или экспериментально) один раз определить положение экстремума, а затем синтезировать обычную систему стабилизации. Во втором и третьем случаях необходимо следить за экстремумом. Если закон дрейфа известен, то может быть использована система программного управления. При неизвестном законе дрейфа обеспечить цель управления может только специальная система поиска экстремума.
Классическим примером системы такого типа является система автоподстройки частоты радиоприемника [12], амплитудная частотная характеристика которой имеет ярко выраженный экстремум (рис. 11.2).
|
Рис. 11.2. Вид АЧХ радиоприемника |
Настройка радиоприемника предполагает поддержание максимума громкости звука или минимума искажений при изменяющихся условиях работы устройства.
Прежде чем говорить о синтезе системы поиска экстремума, необходимо формализовать техническую задачу создания регулятора.
|
Рис. 11.3. Схематичное представление объекта управления |
Будем рассматривать задачу синтеза для объектов, описание которых включает в себя динамическую часть и статическую экстремальную характеристику (модель показателя качества). Обобщенная схема такого объекта управления представлена на рис. 11.3.
Математическая модель объекта имеет вид
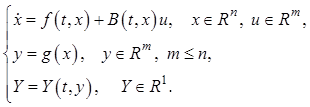(11.1)
Здесь 
– вектор состояния объекта; 
– вектор выходных переменных динамической
части объекта; 
– выходная переменная объекта,
которая представляет собой нелинейную однозначную функцию и имеет экстремум по
переменной ; 
– вектор
нелинейных функций, удовлетворяющих условию существования и единственности
решения дифференциального уравнения; 
– матрица переменных
коэффициентов; 
– вектор-функция, допускающая
многократное дифференцирование.
Зависимость элементов функций 
и
от времени отражает влияние действующих на
объект возмущений, а зависимость 
от t – дрейф
экстремума во времени.
Характер изменения параметров динамической части объекта
и заранее
неизвестен, кроме их граничных значений: 
.
Предполагается также, что темп изменения величин 
, и на
порядок медленнее основных процессов в объекте.
Рассмотрим некоторые наиболее часто
встречающиеся модели статической экстремальной характеристики Y(t,y).
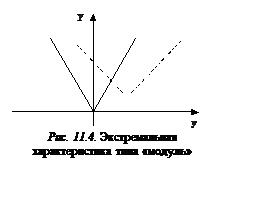
1. Экстремальная характеристика типа «модуль» приведена на рис. 11.4. Она описывается уравнением Y = ½y½.
В общем случае уравнение экстремальной характеристики типа «модуль» имеет вид
. (11.2)
Уравнение (11.2) содержит параметры, отражающие изменение экстремальной характеристики во времени: k1(t) – наклон ветвей характеристики; y0(t) – горизонтальный дрейф экстремума; Y0(t) – вертикальный дрейф экстремальной характеристики.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
